早教吧作业答案频道 -->数学-->
已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.(1)发现与证明:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:当E点旋转到CB的延长线上时(如图2
题目详情
已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.
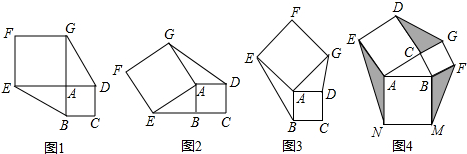
(1)发现与证明:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:___
当E点旋转到CB的延长线上时(如图2),△ABE与△ADG的面积关系是:___
(2)引申与运用:当正方形AEFG旋转任意一个角度时(如图3),△ABE与△ADG的面积关系是___
并证明.
运用:已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图4),则图中阴影部分的面积和的最大值是___cm2.

(1)发现与证明:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:___
当E点旋转到CB的延长线上时(如图2),△ABE与△ADG的面积关系是:___
(2)引申与运用:当正方形AEFG旋转任意一个角度时(如图3),△ABE与△ADG的面积关系是___
并证明.
运用:已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图4),则图中阴影部分的面积和的最大值是___cm2.
▼优质解答
答案和解析
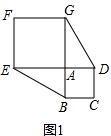 (1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,
(1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,
∴AE=AG,AB=AD,∠EAB=∠GAD,
∴△ABE≌△ADG(SAS),
∴△ABE的面积=△ADG的面积;
②作GH⊥DA交DA的延长线于H,如图2,
∴∠AHG=90°,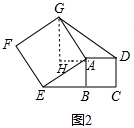
∵E点旋转到CB的延长线上,
∴∠ABE=90°,∠HAB=90°,
∴∠GAH=∠EAB,
在△AHG和△AEB中
,
∴△AHG≌△AEB,
∴GH=BE,
∵△ABE的面积=
EB•AB,△ADG的面积=
GH•AD,
∴△ABE的面积=△ADG的面积;
(2)结论仍然成立.理由如下:
作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图3,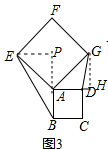
∵∠PAD=90°,∠EAG=90°,
∴∠PAE=∠GAH,
在△AHG和△AEP中
,
∴△AHG≌△AEP(AAS),
∴GH=BP,
∵△ABP的面积=
EP•AB,△ADG的面积=
GH•AD,
∴△ABP的面积=△ADG的面积;
运用:∵AB=5cm,BC=3cm,
∴AC=
=4cm,
∴△ABC的面积=
×3×4=6(cm2);
根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2.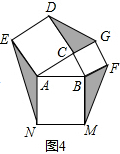
故答案为相等;相等;相等;18.
 (1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,
(1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,∴AE=AG,AB=AD,∠EAB=∠GAD,
∴△ABE≌△ADG(SAS),
∴△ABE的面积=△ADG的面积;
②作GH⊥DA交DA的延长线于H,如图2,
∴∠AHG=90°,

∵E点旋转到CB的延长线上,
∴∠ABE=90°,∠HAB=90°,
∴∠GAH=∠EAB,
在△AHG和△AEB中
|
∴△AHG≌△AEB,
∴GH=BE,
∵△ABE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABE的面积=△ADG的面积;
(2)结论仍然成立.理由如下:
作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图3,

∵∠PAD=90°,∠EAG=90°,
∴∠PAE=∠GAH,
在△AHG和△AEP中
|
∴△AHG≌△AEP(AAS),
∴GH=BP,
∵△ABP的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABP的面积=△ADG的面积;
运用:∵AB=5cm,BC=3cm,
∴AC=
| AB2-BC2 |
∴△ABC的面积=
| 1 |
| 2 |
根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2.

故答案为相等;相等;相等;18.
看了已知正方形ABCD和正方形AE...的网友还看了以下:
有a、b、c、d、e、f、g七种物质.a为HCl,f的元素质量比为7:3.a能与b、f、d反应,c 2020-05-02 …
已知f(x)=e^x-e^﹣x,g(x)=e^x+e^﹣x(e=2.718…).设f(x)·f(y 2020-05-16 …
已知f(x)=e^x-e^-x,g(x)=e^x+e^-x(e=2.718……)(1)求【f(x) 2020-05-16 …
急化学推断题ABCDEFG是常见的7种物质,A是含有2种元素的固体化合物,C是一切生命都离不开的氧 2020-05-20 …
纵横字谜之英语暑假作业题(s)(o)(r)(r)(n)(g)(r)(e))(a)(k)(k)(e) 2020-06-06 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
三元一次方程组a*x+b*y+c*z+d=0,e*x+f*y+g*z+h=0,i*x+j*y+k* 2020-08-03 …
各位帮我解一题九宫图用0到9的数字填进九宫图的A到IABCDEFGHI要求:A+B+C=D+E+F= 2020-11-02 …
我国北方处于平衡状态的某森林生态系统,其碳素循环如图所示,箭头和字母分别表示碳素传递方向和转移量.下 2020-11-07 …
1、已知二叉树的前序遍历序列和中序遍历序列分别是:B,A,C,D,F,E,G和D,C,A,F,G,E 2020-12-05 …