早教吧作业答案频道 -->数学-->
(1)如图①,∠CEF=90°,点B在射线EF上,AB∥CD.若∠ABE=130°,求∠C的度数;(2)如图②,把“∠CEF=90°”改为“∠CEF=120°”,AB∥CD.猜想∠ABE与∠C的数量关系,并说明理由;(3
题目详情
(1)如图①,∠CEF=90°,点B在射线EF上,AB∥CD.若∠ABE=130°,求∠C的度数;
(2)如图②,把“∠CEF=90°”改为“∠CEF=120°”,AB∥CD.猜想∠ABE与∠C的数量关系,并说明理由;(3)如图③,在(2)的条件下,作GC⊥CE,垂足为C,反向延长CD至H,若∠GCH=θ,则∠ABE=___(请用含θ的式子表示).
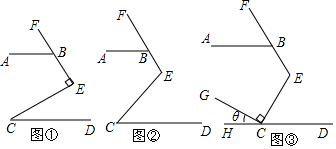
(2)如图②,把“∠CEF=90°”改为“∠CEF=120°”,AB∥CD.猜想∠ABE与∠C的数量关系,并说明理由;(3)如图③,在(2)的条件下,作GC⊥CE,垂足为C,反向延长CD至H,若∠GCH=θ,则∠ABE=___(请用含θ的式子表示).

▼优质解答
答案和解析
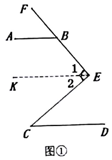 (1)如图①,过E作EK∥AB,则∠ABE+∠1=180°,
(1)如图①,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°-∠ABE=50°,
∵∠CEF=90°,
∴∠2=90°-∠1=40°,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2=40°;
(2)∠ABE-∠C=60°,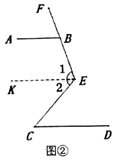
理由:如图②,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°-∠ABE,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2,
∵∠CEF=∠1+∠2=120°,即180°-∠ABE+∠C=120°,
∴∠ABE-∠C=180°-120°=60°;
(3)如图③,过E作EK∥AB,则∠ABE+∠KEB=180°,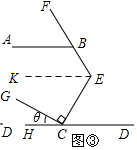
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠DCE+∠KEC=180°,
∴∠ABE+∠BEC+∠DCE=360°,
又∵GC⊥CE,∠GCH=θ,∠CEF=120°,
∴∠ABE+120°+90°+θ=360°,
∴∠ABE=150°-θ.
故答案为:150°-θ.
 (1)如图①,过E作EK∥AB,则∠ABE+∠1=180°,
(1)如图①,过E作EK∥AB,则∠ABE+∠1=180°,∴∠1=180°-∠ABE=50°,
∵∠CEF=90°,
∴∠2=90°-∠1=40°,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2=40°;
(2)∠ABE-∠C=60°,

理由:如图②,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°-∠ABE,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2,
∵∠CEF=∠1+∠2=120°,即180°-∠ABE+∠C=120°,
∴∠ABE-∠C=180°-120°=60°;
(3)如图③,过E作EK∥AB,则∠ABE+∠KEB=180°,

∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠DCE+∠KEC=180°,
∴∠ABE+∠BEC+∠DCE=360°,
又∵GC⊥CE,∠GCH=θ,∠CEF=120°,
∴∠ABE+120°+90°+θ=360°,
∴∠ABE=150°-θ.
故答案为:150°-θ.
看了(1)如图①,∠CEF=90°...的网友还看了以下:
“定义在R上的奇函数f(x)一定满足关系式()”,请求详解(A)f(x)-f(-x)>0(B)f( 2020-04-26 …
高数改错题指出以下过程的错误之处.已知二元函数f(x,y)在x轴和y轴上函数值为1,其它所有点函数 2020-05-13 …
函数在0到1的闭区间内二阶导数大于0选择:a.f'(1)>f'(0)>f(1)—f(0)b.f'( 2020-05-16 …
已知定义在R上的奇函数f(x),满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则() 2020-06-03 …
已知函数y=f(x)是偶函数,y=f(x-2)在[0,2]上是单调减函数,则()A.f(0)<f( 2020-06-26 …
设f(x)是增函数,分别指出d>0或d<0时[f(Xo+d)-f(Xo)]/d的符号.设f(x)是 2020-07-09 …
设f(x)在0,1上满足f''(x)>0,则必有A.f'(1)>f'(0)>f(1)-f(0)B. 2020-07-26 …
已知f'(x)在点x=0处连续,且lim(x→0)[f'(x)/ln(1+x)]=-1,则A.f( 2020-07-31 …
设f(x)在x=0的某邻域内存在二阶导数,且f'(x)=0,lim(x→0)f''(x)/|x|= 2020-07-31 …
函数f(x)的定义域为D,若对于任意x1、x2∈D,当x1<x2时,都有f(x1)≤f(x2),则 2020-08-01 …