如图1，已知：已知：等边△ABC，点D是边BC上一点（点D不与点B、点C重合），求证：BD+DC>AD．下面的证法供你参考：把△ACD绕点A顺时针旋转60°得到△ABE，连接ED，则有△ACD≌△ABE，DC=EB，∵A

Question

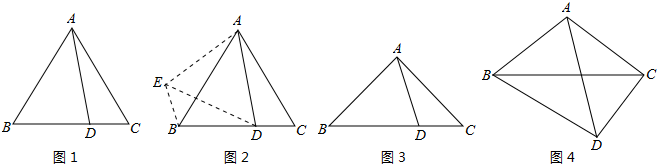
如图1，已知：已知：等边△ABC，点D是边BC上一点（点D不与点B、点C重合），求证：BD+DC>AD．
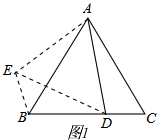
下面的证法供你参考：把△ACD绕点A顺时针旋转60°得到△ABE，连接ED，则有△ACD≌△ABE，DC=EB，
∵AD=AE，∠DAE=60°，
∴△ADE是等边三角形，∴AD=DE．在△DBE中，BD+EB>DE，即：BD+DC>AD
实践探索：
（1）请你仿照上面的思路，探索解决下面的问题：
如图3，点D是等腰直角三角形△ABC边上的点（点D不与B、C重合）．求证：BD+DC>√(2)AD．
（2）如果点D运动到等腰直角三角形△ABC边BC所在直线上时，BD、DC和AD之间又存在怎样的数量关系？直接写出结论．
创新应用：
（3）已知：如图4，等腰△ABC中，AB=AC，且∠BAC=α（α为钝角），D是等腰△ABC外一点，且∠BDC+∠BAC=180°，BD、DC与AD之间存在怎样的数量关系？写出你的猜想，并证明．

Answer 1

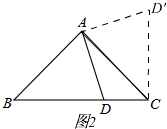
（1）证明：如图1，

把△ACD绕点A顺时针旋转90°得到△ABE，
则有△ACD≌△ABE，DC=EB
∵AD=AE，∠DAE=90°
∴△ADE是等腰直角三角形
∴DE=√(2)AD
在△DBE中，BD+EB>DE，
即：BD+DC>√(2)AD；
（2）如图2，

把△ABD旋转，使AB与AC重合，得到△ACD′，
则BD=CD′，
在△CDD′中，CD+CD′>DD′，
即：BD+CD>DD′，
∵△ADD′是钝角三角形，则DD′>√(2)AD，
当D运动到B的位置时，DD′=BC=AD．
∴BD+DC≥√(2)AD；
（3）猜想1：BD+DC<2AD
证明：如图3，

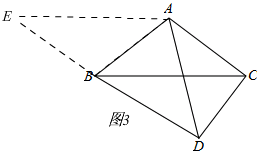
把△ACD绕点A顺时针旋转α，得到△ABE
则有△ACD≌△ABE，DC=EB，∠ACD=∠ABE
∵∠BAC+∠BDC=180°
∴∠ABD+∠ACD=180°
∴∠ABD+∠ABE=180°
即：E、B、D三点共线．
∵AD=AE，
∴在△ADE中，AE+AD>ED，
即BD+DC<2AD．