早教吧作业答案频道 -->数学-->
如图,将等腰直角三角板放在正方形ABCD的顶点B处,且三角板中BE=EF.连AE,再作EG⊥AE且EG=AE.绕点B旋转三角板,并保证线段FG与正方形的边CD交于点H.(1)求证:△ABE≌△GFE.(2)当DH取得
题目详情
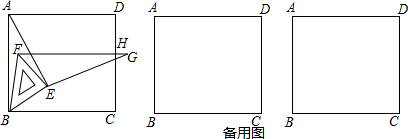
如图,将等腰直角三角板放在正方形ABCD的顶点B处,且三角板中BE=EF.连AE,再作EG⊥AE且EG=AE.绕点B旋转三角板,并保证线段FG与正方形的边CD交于点H.
(1)求证:△ABE≌△GFE.
(2)当DH取得最小值时,求∠ABE的度数.
(3)当三角板有两个顶点在边BC上时,求
的值.
(1)求证:△ABE≌△GFE.
(2)当DH取得最小值时,求∠ABE的度数.
(3)当三角板有两个顶点在边BC上时,求
| GH |
| EF |

▼优质解答
答案和解析
(1)证明:在△ABE和△GFE中,
,
∴△ABE≌△GFE,
(2)∵△ABE≌△GFE,
∴∠BAE=∠BGN,
∵∠AMN=∠EMG,
∴∠ANM=∠MEG=90°,
∴MH⊥AB,
同理得,DH=AN,
要使DH最小,则BN最大,
∵BN≤BF,
∴当BF与BN重合时,AN最小,
∴∠ABE=∠FBE=45°
(3)在△APE和△ECG中,
,
∴△APE≌△ECG,
∴GH=BF,
∴∠ECG=APE=135°
∴△HCG是等腰直角三角形,
∴HG=CH=FE,
∴
=1,
∵FG=AB=BC,
∴HG=BF,
∴
=
.
|
∴△ABE≌△GFE,
(2)∵△ABE≌△GFE,
∴∠BAE=∠BGN,
∵∠AMN=∠EMG,
∴∠ANM=∠MEG=90°,
∴MH⊥AB,
同理得,DH=AN,
要使DH最小,则BN最大,
∵BN≤BF,
∴当BF与BN重合时,AN最小,
∴∠ABE=∠FBE=45°
(3)在△APE和△ECG中,
|
∴△APE≌△ECG,
∴GH=BF,
∴∠ECG=APE=135°
∴△HCG是等腰直角三角形,
∴HG=CH=FE,
∴
| HG |
| EF |
∵FG=AB=BC,
∴HG=BF,
∴
| GH |
| EF |
| 2 |
看了如图,将等腰直角三角板放在正方...的网友还看了以下:
如图,在梯形ABCD中,AB‖CD,∠A=90°,AB=3,CD=6,BE⊥BC交直线AD于点E. 2020-05-15 …
如图,在直线坐标系中,直线y=-4/3x+4与y轴,x轴分别交于A,B两点,且AB=5.点C的坐标 2020-05-16 …
如图所示,菱形ABCD的对角线相交于点O,AE∥BD,BE∥AC,AE,BE相交于点E,当菱形AB 2020-05-17 …
在△ABC中,角BAC=90°,AD⊥BC于点D,点O是AC边上一点,连BO交AD于点F,OE⊥O 2020-06-06 …
角ACD是角ABC的一个外角,角ABC的平分线和角ACD的平分线相交于点E.当角A=80度时,求角 2020-06-07 …
如图,在梯形ABCD中,AB‖CD,∠A=,AB=3,CD=6,BE⊥BC交直线AD于点E.(1) 2020-06-12 …
在三角形ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF平行AC交AC于点F,DE平行 2020-06-12 …
已知:如图,A,K是圆O上的两点,直线FN垂直于MA,垂足为N,FN与圆O相切与点F,角AOK=2角 2020-10-31 …
当B等于Y时,A等于Z;当A不等于Z时,E要麽等于Y,要麽等于Z,所以?A:当B等于Y时,E既不等于 2020-12-03 …
是一种医药中间体,常用来制备抗凝血药,可通过下列路线合成已知:E变成F相当于在E分子中去掉1个X分子 2020-12-14 …