早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,点E为AC上一点,且∠DEB=120°(1)求证:△ADE≌△ABE;(2)若∠DAB=60°,AD=23,求DE的长.
题目详情
如图,在菱形ABCD中,点E为AC上一点,且∠DEB=120°
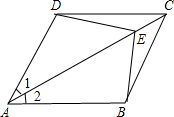
(1)求证:△ADE≌△ABE;
(2)若∠DAB=60°,AD=2
,求DE的长.

(1)求证:△ADE≌△ABE;
(2)若∠DAB=60°,AD=2
| 3 |
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是菱形,
∴AD=AB,∠1=∠2,
在△ADE和△ABE中
,
∴△ADE≌△ABE(SAS);
(2)∵△ADE≌△ABE,
∴∠1=∠2=
∠DAB=30°,
∠DEA=
∠DEB=60°,
∴∠ADE=90°,
在△DAE中,设DE=x,AE=2x,
由勾股定理得:AD2+DE2=AE2,
即(2
)2+x2=(2x)2,
解得:x=2,
∴DE=2.
∴AD=AB,∠1=∠2,
在△ADE和△ABE中
|
∴△ADE≌△ABE(SAS);
(2)∵△ADE≌△ABE,
∴∠1=∠2=
| 1 |
| 2 |
∠DEA=
| 1 |
| 2 |
∴∠ADE=90°,
在△DAE中,设DE=x,AE=2x,
由勾股定理得:AD2+DE2=AE2,
即(2
| 3 |
解得:x=2,
∴DE=2.
看了如图,在菱形ABCD中,点E为...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
已知椭圆y^2/a^2+x^2/b^2=1(a>b>0)的右顶点为A(1,0)过其焦点且垂直长轴的 2020-04-06 …
已知二次函数y=x*x+4x与x轴交于B,O两点,顶点为A,连接AB,过原点O作AB的平行线得到直 2020-04-27 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
有一质点由A向B运动,A、B间距离为L,已知质点在A的速度为V0,加速度为a,如果将有一质点由A向 2020-05-17 …
已知函数f(x)=x^3+x-16.直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切 2020-05-20 …
设集合M={平面内的点(a,b)},N={f(x)|f(x)=acos2x+bsin2x,x∈R} 2020-06-02 …
已知点F1是抛物线C:x2=2py(p>0)的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2 2020-06-16 …
点A、B、C在数轴上对应的数分别为1、3、5,点P在数轴上对应的数是-2,点P关于点A的对称点为P 2020-06-19 …