早教吧作业答案频道 -->数学-->
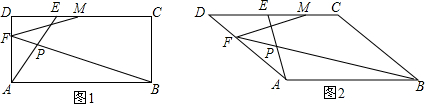
如图1,在矩形ABCD中,点E为矩形的边CD上任意一点,点P为线段AE的中点,连接BP并延长交边AD于点F,点M为边CD上一点,连接FM,且∠DMF=∠ABF.(1)若AD=2,DE=1,求AP的长;(2)求证:PB=PF+FM;
题目详情
如图1,在矩形ABCD中,点E为矩形的边CD上任意一点,点P为线段AE的中点,连接BP并延长交边AD于点F,点M为边CD上一点,连接FM,且∠DMF=∠ABF.
(1)若AD=2,DE=1,求AP的长;
(2)求证:PB=PF+FM;
(3)若矩形ABCD改为▱ABCD,如图2,(2)中的结论成立吗?若成立,请证明;不成立,说明理由.
(1)若AD=2,DE=1,求AP的长;
(2)求证:PB=PF+FM;
(3)若矩形ABCD改为▱ABCD,如图2,(2)中的结论成立吗?若成立,请证明;不成立,说明理由.

▼优质解答
答案和解析
(1) ∵四边形ABCD为矩形,∴∠ADE=90°,∴AE=AD2+DE2=22+12=5,∵点P为线段AE的中点,∴AP=PE=12AE=12×5=52;(2)证明:延长BF、CD交于点N,如图1所示:∵四边形ABCD为矩形,∴CN∥AB,∴∠N=∠PBA,∠NEP=∠BA...
看了如图1,在矩形ABCD中,点E...的网友还看了以下:
一道高难度的数学题等边三角形的边长a=√25+(12√3),点P是△ABC内的一点,且PA²+PB 2020-04-26 …
如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬 2020-04-27 …
三角形的面积公式是什么?三角形公式不是(底乘高)/2吗?为什么又有s=((d-a)(d-b)(d- 2020-05-13 …
正方形ABCD的边长为a,PA垂直于ABCD,且PA=a,求二面角A-PB-C,B-PC-D的大小 2020-05-16 …
.三角形PAB中,PA垂直PB,PA=a,PB=b三角形PAB中,PA垂直PB,PA=a,PB=b 2020-05-19 …
(2014•广安二模)如图,在四棱椎P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2的 2020-06-21 …
二面角的问题已知边长喂a的正方形ABCD外有一点P,使PA垂直平面ABCD,PA=a,求二面角A- 2020-06-27 …
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=23,E是 2020-07-18 …
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,E、F分别是PB、C 2020-07-31 …
立体几何,火速ABCD是边长为1的正方形,PD垂直平面ABCD,PD=3E是棱PB上一点,过点AD 2020-08-02 …