早教吧作业答案频道 -->数学-->
如图,点A、B、C在⊙O上,∠ABO=30°,∠ACO=45°,则∠BOC等于()A、60°B、90°C、150°D、160°
题目详情
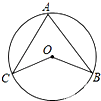 如图,点A、B、C在⊙O上,∠ABO=30°,∠ACO=45°,则∠BOC等于( )
如图,点A、B、C在⊙O上,∠ABO=30°,∠ACO=45°,则∠BOC等于( )| A、60° | B、90° |
| C、150° | D、160° |
▼优质解答
答案和解析
考点:
圆周角定理
专题:
分析:
过A、O作⊙O的直径AD,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质求出∠BOC=2∠ABO+2∠ACO.
过A作⊙O的直径,交⊙O于D;在△OAB中,OA=OB,则∠BOD=∠ABO+∠OAB=2×30°=60°,同理可得:∠COD=∠ACO+∠OAC=2×45°=90°,故∠BOC=∠BOD+∠COD=150°.故选C.
点评:
本题考查了圆周角定理,涉及了等腰三角形的性质及三角形的外角性质,解答本题的关键是求出∠COD及∠BOD的度数.
考点:
圆周角定理
专题:
分析:
过A、O作⊙O的直径AD,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质求出∠BOC=2∠ABO+2∠ACO.
过A作⊙O的直径,交⊙O于D;在△OAB中,OA=OB,则∠BOD=∠ABO+∠OAB=2×30°=60°,同理可得:∠COD=∠ACO+∠OAC=2×45°=90°,故∠BOC=∠BOD+∠COD=150°.故选C.
点评:
本题考查了圆周角定理,涉及了等腰三角形的性质及三角形的外角性质,解答本题的关键是求出∠COD及∠BOD的度数.
看了如图,点A、B、C在⊙O上,∠...的网友还看了以下:
如图(a)所示直角三角板ABC的边长BC=a,AC=b,开始时AB边靠在y轴上,B与坐标原点O重合 2020-04-06 …
你知道方格纸上图形的位置关系吗?(1)图形B可以看作图形A绕点顺时针方向旋转90°得到的.(2)图 2020-04-06 …
你知道方格纸上图形的位置关系吗?(1)图形B可以看作图形A绕点顺时针方向旋转90°得到的.(2)图 2020-05-13 …
如图所示中,图形B可以看作是由图形A绕点顺时针旋转90°得到的.图形C可以看作是由图形B绕点O顺时 2020-05-13 …
如图所示,△A′O′B′表示水平放置的△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A 2020-06-27 …
如图(a)所示直角三角板ABC的边长BC=a,AC=b,开始时AB边靠在y轴上,B与坐标原点O重合 2020-07-19 …
如图,已知:点A、点B及直线l.(1)请画出从点A到直线l的最短路线,并写出画图的依据.(2)请在 2020-07-21 …
如图所示,△A′O′B′表示水平放置△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′ 2020-08-01 …
观察方格纸上所画图形的位置,并填空.(1)图形B可以看作图形A绕点O顺时针方向旋转得到的;(2)图形 2020-11-03 …
那新疆2013中考数学的23题呢?刚刚问的是24题,如图,已知⊙O的半径为4,CD是⊙O的直径,AC 2021-01-22 …