早教吧作业答案频道 -->数学-->
如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为1,2,3,将△ABP绕点B旋转至△CBP′,连接PP′.(1)求证:△BPP′是等腰直角三角形;(2)求∠APB的度数.
题目详情
如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为1,2,3,将△ABP绕点B旋转至△CBP′,连接PP′.
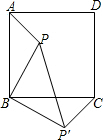
(1)求证:△BPP′是等腰直角三角形;
(2)求∠APB的度数.

(1)求证:△BPP′是等腰直角三角形;
(2)求∠APB的度数.
▼优质解答
答案和解析
(1)证明:∵将△ABP绕点B旋转至△CBP′,
∴△ABP≌△CBP′,
∴∠PBP′=∠ABC=90°,BP=BP′=2,P′C=AP=1,∠APB=∠BP′C
∴△BPP′为等腰直角三角形;
(2) 连接PC,如图所示: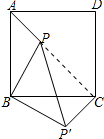
由(1)得:△BPP′为等腰直角三角形,
∴∠BP′P=45°,PP′=
=2
,
∵PP′2+P′C2=8+1=9=PC2,
∴△BP′C是直角三角形,∠PP′C=90°,
∴∠APB=∠BP′C=90°+45°=135°.
∴△ABP≌△CBP′,
∴∠PBP′=∠ABC=90°,BP=BP′=2,P′C=AP=1,∠APB=∠BP′C
∴△BPP′为等腰直角三角形;
(2) 连接PC,如图所示:

由(1)得:△BPP′为等腰直角三角形,
∴∠BP′P=45°,PP′=
| 22+22 |
| 2 |
∵PP′2+P′C2=8+1=9=PC2,
∴△BP′C是直角三角形,∠PP′C=90°,
∴∠APB=∠BP′C=90°+45°=135°.
看了如图,点P是正方形ABCD内一...的网友还看了以下:
下列有关羟基(-OH)与氢氧根(OH-)的说法不正确的是()A.-OH是不显电性的自由基,OH-是 2020-04-11 …
下列有关羟基(-OH)与氢氧根(OH-)的说法不正确的是A.-OH是不显电性的自由基,OH-是显电 2020-04-11 …
初三数学题在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,3),B(-4,-3)C(2,- 2020-05-13 …
设随机变量X,Y相互独立,其概率密度函数分别为:.求:D(X),D(Y)和D(X-Y)其函数密度韩 2020-05-15 …
已知数轴上A、B两点坐标分别为-3、-6,若在数轴找一点C,使得A与C的距离为4.找一点D,使得B 2020-05-16 …
(2014•崇明县一模)已知4个连锁基因的交换值分别是:A和B为40%,B和C为20%,C和D为1 2020-05-17 …
下列物质中,可一次性鉴别乙酸、乙醇、苯及氢氧化钡溶液的是A.金属钠 B.溴水 C.碳酸钠 D.水我 2020-05-17 …
两道道基础的积分题∫(5X+2)/(1+2X^2)DX∫sin^3(X)dx(SINX的立方)不知 2020-05-20 …
有谁知道这首英文诗的名字吗,最好有全文谢谢!是一首英文诗,我原来在疯狂英语上读过,但是因为是别人的 2020-06-19 …
9EDTA二钠盐(Na2H2Y)水溶液pH约是(D)(已知EDTA的各级解离常数分别为10-9ED 2020-07-13 …