早教吧作业答案频道 -->数学-->
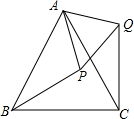
如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.(1)求证:△ABP≌△ACQ.(2)判断△APQ的形状,并说明理由.
题目详情
如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ.
(2)判断△APQ的形状,并说明理由.

(1)求证:△ABP≌△ACQ.
(2)判断△APQ的形状,并说明理由.
▼优质解答
答案和解析
(1)证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵
,
∴△ABP≌△ACQ(SAS);
(2) △APQ为等边三角形,
理由:∵△ABP≌△ACQ,
∴AP=AQ,∠BAP=∠CAQ,
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
∴AB=AC.
在△ABP与△ACQ中,
∵
|
∴△ABP≌△ACQ(SAS);
(2) △APQ为等边三角形,
理由:∵△ABP≌△ACQ,
∴AP=AQ,∠BAP=∠CAQ,
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
看了如图,等边△ABC中,点P在△...的网友还看了以下:
在循环双链表的p所指节点之后插入s所直接点操作A,p->next=s;s->prior=p;p->n 2020-03-31 …
已知关于x的方程x的平方+px+q=0的两个实数根为p,q.求p,q的值将p,q分别代入x²+px 2020-05-16 …
概率中关于事件之间的运算P(AUB)=1,为什么AUB不是全集?P(AUB)=0,为什么AB不是空 2020-05-16 …
概率加法公式加法公式,对于任意两事件A,B,有P(A并B)=P(A)+P(B)-P(AB)成立,假 2020-05-16 …
要解说口头的解说!那我问你,如果有已知的一条直线AB,和一个平面直角坐标系,P点在X轴上,求P点在 2020-05-17 …
俩质量相等实心小球密度分别为P甲P乙且P甲:P乙=3:2将他们放入足够深水中甲乙俩球静止时受浮力比 2020-05-17 …
¬(P↔Q)怎么推出(P∧¬Q)∨(¬P∧Q).古典逻辑.真值树系统推论的一步一步过程详细点.例子 2020-06-12 …
如图所示,当用扳手拧螺母时,扳手上的P、Q两点的角速度分别为ωP和ωQ,线速度大小分别为υP和υQ 2020-06-12 …
两题单链表逆置,求讲解1.p=head->next;head->next=NULL;while(p 2020-06-15 …
1.y''+(y')^2+1=0求通解,我想问这个使用y''=f(x,y')型的算还是用y''=f 2020-06-25 …