早教吧作业答案频道 -->数学-->
综合应用抛物线和双曲线的光学性质,可以设计制造反射式天文望远镜,这种望远镜的特点是,镜筒可以很短而观察天体运动又很清楚.例如,某天文仪器厂设计制造的一种镜筒直径为0.6m,
题目详情
综合应用抛物线和双曲线的光学性质,可以设计制造反射式天文望远镜,这种望远镜的特点是,镜筒可以很短而观察天体运动又很清楚.例如,某天文仪器厂设计制造的一种镜筒直径为0.6m,长为2m的反射式望远镜,其光学系统的原理如图(中心截口示意图)所示.其中,一个反射镜PO1Q弧所在的曲线为抛物线,另一个反射镜MO2N弧所在的曲线为双曲线的一个分支.已知F1,F2是双曲线的两个焦点,其中F2同时又是抛物线的焦点,试根据图示尺寸(单位:mm),分别求抛物线和双曲线的方程.
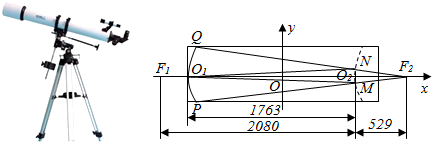

▼优质解答
答案和解析
对于双曲线,有
,∴a=775.5,c=1304.5,
∴b=
,
∴双曲线的方程为
-
=1(x>775.5);
∵抛物线的顶点的横坐标是-(1763-a)=-(1763-775.5)=-987.5,
∴抛物线的方程为y2=9168(x+987.5).
|
∴b=
| 1100320 |
∴双曲线的方程为
| x2 |
| 601400.3 |
| y2 |
| 1100320 |
∵抛物线的顶点的横坐标是-(1763-a)=-(1763-775.5)=-987.5,
∴抛物线的方程为y2=9168(x+987.5).
看了综合应用抛物线和双曲线的光学性...的网友还看了以下:
如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段P 2020-04-08 …
``麻烦给出详细的过程题1:点F为双曲线C的左焦点,左准线L交X轴于点Q,点P是L上的一点,已知| 2020-04-08 …
(直线L过坐标原点O且和双曲线交于两点M,N,点P为双曲线上异于M,N的一点,且直线PM已知双曲线 2020-04-08 …
已知双曲线C的焦点F(3,0),双曲线C上一点P到F的最短距离为3-2.(1)求双曲线的标准方程和 2020-05-13 …
(12分)已知双曲线C以椭圆的焦点为顶点,顶点为焦点(1)求双曲线C的标准方程;(2)若双曲线C的 2020-05-13 …
(2014•太原二模)已知点E(-2,0),F(2,0),曲线C上的动点M满足ME•MF=−3,定 2020-05-15 …
一道圆锥曲线,已知曲线C的方程为y^2=4x(x>0),曲线E是以F1(-1,0)、F(1,0)为 2020-05-15 …
已知双曲线C的中点在原点,双曲线C的右焦点为F坐标为(2,0),且双曲线过点C(2,3).(1)求 2020-05-15 …
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足|+|=·(+ 2020-05-15 …
爱,先于生命,后与死亡,是创造的起点,世界的原型,这句话要表达什么啊 2020-05-22 …