三世纪中期，魏晋时期的数学家刘徽首创割圆术，为计算圆周率建立了严密的理论和完善的算法，所谓割圆术，就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法．按

Question

三世纪中期，魏晋时期的数学家刘徽首创割圆术，为计算圆周率建立了严密的理论和完善的算法，所谓割圆术，就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法．按照这样的思路，刘徽把圆内接正多边形的面积一直算到了正3072边形，并由此而求得了圆周率为3.1415和 3.1416这两个近似数值．如图所示是利用刘徽的割圆术设计的程序框图，若输出的n=24，则p的值可以是（参考数据：

√(3)=1.732，sin15°≈0.2588，sin7.5°≈0.1305，sin3.75°≈0.0654）（　　）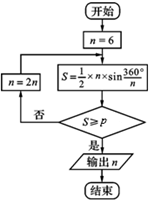

A. 2.6

B. 3

C. 3.1

D. 3.14

Answer 1

模拟执行程序，可得：
n=6，S=3sin60°=(3√(3))/(2)，
不满足条件S≥p，n=12，S=6×sin30°=3，
不满足条件S≥p，n=24，S=12×sin15°=12×0.2588=3.1056，
满足条件S≥p，退出循环，输出n的值为24，
故p=3.1，
故选：C．