早教吧作业答案频道 -->数学-->
如图,点P是直线l外一点,过点P画直线PA、PB、PC、…交l于点A、B、C、…,交l于点A、B、C、…(1)请你用量角器量∠1,∠2,∠3的度数,并度量PA、PB、PC的长度;(2)你发现了什么规律?请
题目详情
如图,点P是直线l外一点,过点P画直线PA、PB、PC、…交l于点A、B、C、…,交l于点A、B、C、…
(1)请你用量角器量∠1,∠2,∠3的度数,并度量PA、PB、PC的长度;
(2)你发现了什么规律?请把你发现的规律写出来;
(3)猜想:当___时,过点P的直线与l的交点的距离最短.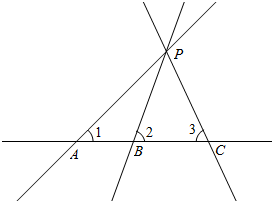
(1)请你用量角器量∠1,∠2,∠3的度数,并度量PA、PB、PC的长度;
(2)你发现了什么规律?请把你发现的规律写出来;
(3)猜想:当___时,过点P的直线与l的交点的距离最短.

▼优质解答
答案和解析
(1)∠1=45°,∠2=70°,∠3=65°,
PA=1厘米,PB=0.7厘米,PC=0.8厘米.
(2)因为∠1=45°,∠2=70°,∠3=65°,
所以∠1<∠3<∠2,
因为PA=1厘米,PB=0.7厘米,PC=0.8厘米,
所以PA>PC>PB,
所以∠1<∠3<∠2,PA>PC>PB,
我发现的规律是:过点P的直线与直线l的夹角越大,则过点P的直线与l的交点的距离越短.
(3)根据过点P的直线与直线l的夹角越大,则过点P的直线与l的交点的距离越短,
猜想:当过点P的直线与直线l的夹角是90°时,过点P的直线与l的交点的距离最短.
故答案为:过点P的直线与直线l的夹角是90°.
PA=1厘米,PB=0.7厘米,PC=0.8厘米.
(2)因为∠1=45°,∠2=70°,∠3=65°,
所以∠1<∠3<∠2,
因为PA=1厘米,PB=0.7厘米,PC=0.8厘米,
所以PA>PC>PB,
所以∠1<∠3<∠2,PA>PC>PB,
我发现的规律是:过点P的直线与直线l的夹角越大,则过点P的直线与l的交点的距离越短.
(3)根据过点P的直线与直线l的夹角越大,则过点P的直线与l的交点的距离越短,
猜想:当过点P的直线与直线l的夹角是90°时,过点P的直线与l的交点的距离最短.
故答案为:过点P的直线与直线l的夹角是90°.
看了如图,点P是直线l外一点,过点...的网友还看了以下:
如图,直线AC∥BD,直线L1、L2分别交AC、BD于A、C、B、D,点P在直线L2上(异于C、D 2020-04-26 …
如图1,在平行四边形ABCD中,AE⊥BC于点E,E恰为BC的中点,tanB=2.;(3)请你在图 2020-05-13 …
认为你是数学帝的看过来.经过点P(4,1)的直线l交双曲线x^2/12-y^2/4=1于A,B两点 2020-05-13 …
(1)在平行四边形ABCD中,点G在BD的延长线上,CD、AD的延长线分别与AG,CG相交于点E, 2020-07-30 …
已知平面上的曲线C及点P,在C上任取一点Q,定义线段PQ长度的最小值为点P到曲线C的距离,记作d( 2020-07-30 …
p是抛物线y∧2=4x上的点,若P到准线的距离是5,则点P的坐标为答案为(4,±4),你们不用算了 2020-07-31 …
(她414•内江模拟)设函数p(x)=13x3-ax(a>4),g(x)=bx她+她b-1.(1)若 2020-11-12 …
如图,点P是直线l外一点,过点P画直线PA、PB、PC、…交l于点A、B、C、…,交l于点A、B、C 2020-11-27 …
作图题(要求:画出图形,保留作图痕迹,并简要说明画法,不要求证明).已知∠AOB及其内部一点P.(1 2021-02-19 …
作图题(要求:画出图形,保留作图痕迹,并简要说明画法,不要求证明).已知∠AOB及其内部一点P.(1 2021-02-19 …