早教吧作业答案频道 -->数学-->
如图,∠ABC=90°,D、E分别在BC,AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.(1)求证:△AFM≌△DFC;(2)AD与MC垂直吗?并说明理由.
题目详情
如图,∠ABC=90°,D、E分别在BC,AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
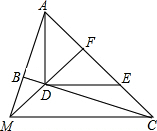
(1)求证:△AFM≌△DFC;
(2)AD与MC垂直吗?并说明理由.

(1)求证:△AFM≌△DFC;
(2)AD与MC垂直吗?并说明理由.
▼优质解答
答案和解析
证明:(1)∵AD⊥DE,AD=DE ,点F是AE的中点,
,点F是AE的中点,
∴∠AFM=∠DFC=90°,AF=DF,∠DEA=∠DAE=45°.
∵∠ABC=∠AFM=90°,
∴∠AMF+∠MAC=90°,∠DCF+∠MAC=90°,
∴∠AMF=∠DCF.
在△AFM和△DFC中,
∴△AFM≌△DFC;
(2)AD⊥MC.
理由如下:
由(1)知,△AFM≌△DFC,
∴FM=FC.
∴△FMC是等腰直角三角形,
∴∠FCM=45°.
∵∠FED=45°,
∴∠FED=∠FCM,
∴DE∥MC.
∵AD⊥DE,
∴AD⊥MC.
 ,点F是AE的中点,
,点F是AE的中点,∴∠AFM=∠DFC=90°,AF=DF,∠DEA=∠DAE=45°.
∵∠ABC=∠AFM=90°,
∴∠AMF+∠MAC=90°,∠DCF+∠MAC=90°,
∴∠AMF=∠DCF.
在△AFM和△DFC中,
|
∴△AFM≌△DFC;
(2)AD⊥MC.
理由如下:
由(1)知,△AFM≌△DFC,
∴FM=FC.
∴△FMC是等腰直角三角形,
∴∠FCM=45°.
∵∠FED=45°,
∴∠FED=∠FCM,
∴DE∥MC.
∵AD⊥DE,
∴AD⊥MC.
看了 如图,∠ABC=90°,D、...的网友还看了以下:
线代,A为n阶方阵A^2-2A-3E=0求(A^2+A+E)^-12.设AB均为正交矩阵|A|=- 2020-04-12 …
1.已知-[-(-a)]=2,求a的相反数.若a-2和-7互为相反数,求a的值.若x,y互为相反数 2020-05-13 …
在平面直角坐标系中,直线y=2x-3上有一动点A,以点A为圆心,3为半径作圆A.(1)当圆A与直线 2020-05-17 …
已知|ab-2|与|a-1|互为相反数求值1/ab+1/(a+1)(b+1)+1/(a+2)(b+ 2020-06-03 …
已知点A的坐标为(2x-1,3y+7),B(x+1,y-5)1.若A点的横坐标是B点的横坐标的3倍 2020-06-14 …
两方阵相加再求逆的表达式问题两个方阵相加再求逆化为其中一个方阵的逆阵和一个新方阵的和,求该新方阵的 2020-06-18 …
已知平面上3个向量a,b,c的模长均为1,它们相互间的夹角均相同(1)求证:(a-b)⊥c(2已知 2020-07-07 …
问几题有理数的问题1、已知-{--(-a)}=2,则a的相反数是2、已知2n-3与-9互为相反数,求 2020-12-24 …
已知-{-(-a)}等于2求a的相反值若a-2和-7为相反数,求a的值若x,y互为相反数,求2010 2020-12-31 …
⑴若m/3+1与2m-7/3互为相反数,求m的值.⑵关于x的方程(a的立方+8a-15)x=2a的立 2020-12-31 …