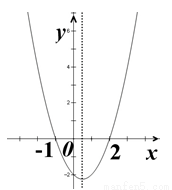
二次函数y=a+bx+c（a≠0）的大致图象如图所示，关于该二次函数，下列说法错误的是（）A、函数有最小值B、对称轴是直线x=C、当x＜y随x的增大而减小D、当－1＜x＜2

Question

二次函数y=a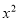 +bx+c（a≠0）的大致图象如图所示，关于该二次函数，下列说法错误的是（ ）

A、函数有最小值

B、对称轴是直线x=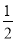

C、当x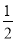＜ y随x的增大而减小

D、当－1＜x＜2 时y＞0

Answer 1

D

分 析：
根据图示可得函数有最小值；对称轴为直线x=；当x＜时，y随x的增大而减小；当－1＜x＜2时，y＜0.
考点：
二次函数的性质. 考点
分析：
考点1：二次函数 定义： 一般地，如果（a，b，c是常数，a≠0），那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2; ②二次函数（a≠0）中x、y是变量，a，b，c是常数，自变量x 的取值范围是全体实数，b和c可以是任意实数，a是不等于0的实数，因为a=0时，变为y=bx+c若b≠0 则y=bx+c是一次函数，若b=0，则y=c是一个常数函数。 ③二次函数（a≠0）与一元二次方程（a≠0）有密切联系，如果将变量y换成一个常数，那么这个二次函数就是一个一元二次函数。 二次函数的解析式有三种形式： （1）一般式：（a，b，c是常数，a≠0）； （2）顶点式： （a，h，k是常数，a≠0） （3）当抛物线与x轴有交点时，即对应二次好方程有实根x1和x2存在时，根据二次三项式的分解因式，二次函数可转化为两根式。如果没有交点，则不能这样表示。 二次函数的一般形式的结构特征： ①函数的关系式是整式； ②自变量的最高次数是2； ③二次项系数不等于零。 二次函数的判定： 二次函数的一般形式中等号右边是关于自变量x的二次三项式； 当b=0，c=0时，y=ax2是特殊的二次函数； 判断一个函数是不是二次函数，在关系式是整式的前提下，如果把关系式化简整理（去括号、合并同类项）后，能写成（a≠0）的形式，那么这个函数就是二次函数，否则就不是。 试题属性 题型： 难度： 考核： 年级