早教吧作业答案频道 -->数学-->
已知函数f(x)=log3x-1x+1,g(x)=-2ax+a+1.(1)当a=-1时,记h(x)=f(x)+g(x).①求证:h(x)为奇函数;②直接写出函数h(x)的单调区间以及函数h(x)的零点个数(不必证明);(2)
题目详情
已知函数f(x)=log3
,g(x)=-2ax+a+1.
(1)当a=-1时,记h(x)=f(x)+g(x).
①求证:h(x)为奇函数;
②直接写出函数h(x)的单调区间以及函数h(x)的零点个数(不必证明);
(2)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
| x-1 |
| x+1 |
(1)当a=-1时,记h(x)=f(x)+g(x).
①求证:h(x)为奇函数;
②直接写出函数h(x)的单调区间以及函数h(x)的零点个数(不必证明);
(2)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
▼优质解答
答案和解析
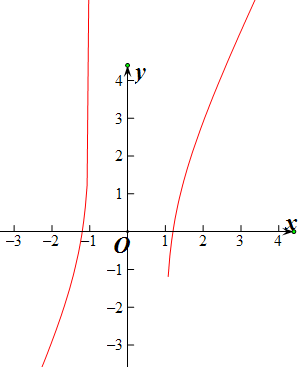 ∵函数f(x)=log3
∵函数f(x)=log3
,g(x)=-2ax+a+1.
(1)①当a=-1时,记h(x)=f(x)+g(x).
h(x)=log3
+2x,
>0,x>1或x<-1,
h(-x)=log3
-2x=-log3
-2x=-h(x),
∴h(x)为奇函数;
②y=
=1-
在(1,+∞)与(-∞,-1)上单调递增,
y=2x是增函数,
h(x)的定义域为:(-∞,-1)∪(1,+∞)
h(x)有2个零点,
h(x)在(1,+∞)与(-∞,-1)上单调递增,
(2)关于x的方程f(x)=log3g(x)有两个不等实数根,
log3
=log3g(x),
即
=-2ax+a+1.x∈(-∞,-1)∪(1,+∞)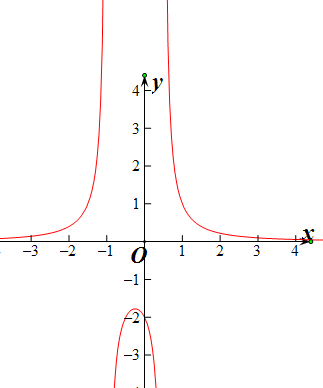
=a(-2x+1),
a=
,
y=
,
x=-
时,y=-
,
运用图象可判断出y=a,与y=
,有2个交点,
实数a的取值范围:a>0或a<-
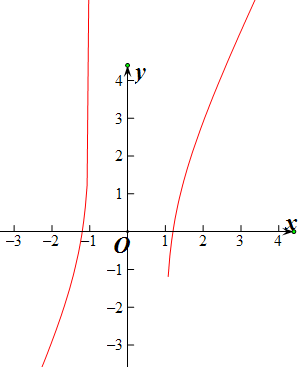 ∵函数f(x)=log3
∵函数f(x)=log3| x-1 |
| x+1 |
(1)①当a=-1时,记h(x)=f(x)+g(x).
h(x)=log3
| x-1 |
| x+1 |
| x-1 |
| x+1 |
h(-x)=log3
| -x-1 |
| -x+1 |
| x-1 |
| x+1 |
∴h(x)为奇函数;
②y=
| x-1 |
| x+1 |
| 2 |
| x+1 |
y=2x是增函数,
h(x)的定义域为:(-∞,-1)∪(1,+∞)
h(x)有2个零点,
h(x)在(1,+∞)与(-∞,-1)上单调递增,
(2)关于x的方程f(x)=log3g(x)有两个不等实数根,
log3
| x-1 |
| x+1 |
即
| x-1 |
| x+1 |

| -2 |
| x+1 |
a=
| 2 |
| (x+1)(2x-1) |
y=
| 2 |
| (x+1)(2x-1) |
x=-
| 1 |
| 2 |
| 16 |
| 9 |
运用图象可判断出y=a,与y=
| 2 |
| (x+1)(2x-1) |
实数a的取值范围:a>0或a<-
| 16 |
| 9 |
看了 已知函数f(x)=log3x...的网友还看了以下:
下列各式中,是整式的有()①−14x2;②3xy+2y-3;③y2x;④x2y−13x2;⑤3x+ 2020-04-22 …
人类正常情况下,精子内的染色体数目和类型是()①44+XY②44+XX③22+Y④22+X.A.① 2020-05-12 …
已知函数f(x)=lnx,g(x)=ax2-x(a≠0).(1)设F(x)=f(x)-g(x)在[ 2020-06-12 …
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)().A.无极大值点,有四 2020-07-08 …
若z=(),则有∂z∂x=∂f∂x.A.f(x,y2)B.f(x2,y)C.f(x,x+y)D.f 2020-07-16 …
下列各式,属于二元一次方程的个数有()①xy+2x-y=7;②4x+1=x-y;③1x+y=5;④ 2020-07-29 …
对于下列说法,错误的个数是①是分式;②当x≠1时,成立;③当x=-3时,分式的值是零;④a;⑤;⑥ 2020-07-29 …
设函数f(x)在闭区间[a,b]上连续并在开区间(a,b)内可导,如果在(a,b)内f′(x)>0 2020-08-01 …
打官司指的是(),是人民法院主持有利害关系人参与的处理纠纷的程序.A.调解B.诉讼C.公证D.仲裁 2020-12-21 …
有X、Y、Z三种金属,能发生以下置换反应:则X、Y、Z三种金属的活动性由强到弱的顺序可排列为()①X 2021-01-07 …