早教吧作业答案频道 -->数学-->
(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证
题目详情
(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.
(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.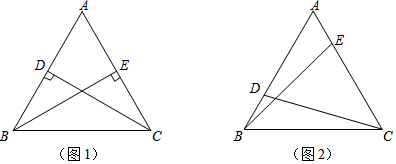
(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.

▼优质解答
答案和解析
(1)证明:∵CD⊥AB于点D,BE⊥AC,
∴∠AEB=∠ADC=90°,
在△ABE与△ACD中,
,
∴△ABE≌△ACD(AAS).
∴CD=BE;
(2)CD=BE,
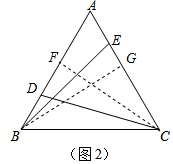
证明如下:分别作CF⊥AB,BG⊥AC,
∴∠CBF=90°,∠BGC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中,
,
∴△FBC≌△GCB.
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中,
,
∴△CFD≌△BGE,
∴CD=BE.
∴∠AEB=∠ADC=90°,
在△ABE与△ACD中,
|

∴△ABE≌△ACD(AAS).
∴CD=BE;
(2)CD=BE,
证明如下:分别作CF⊥AB,BG⊥AC,
∴∠CBF=90°,∠BGC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中,
|
∴△FBC≌△GCB.
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中,
|
∴△CFD≌△BGE,
∴CD=BE.
看了(1)如图1,在△ABC中,A...的网友还看了以下:
已知数集A满足条件:若a属于A,a不等于1,则1/1+a属于A 若0属于A,则在A中还有什么元素若 2020-04-06 …
数学“基本不等式及其应用”的问题最近学习遇到瓶颈,这一块东西始终无法掌握,有什么办法?如此题,我一 2020-05-14 …
矩阵A,B有A^2+B^2=E且|A|+|B|=0;求证|A+B|=0 2020-05-22 …
已知a+b+c>0,ab+bc+ac>0,abc>0,用反证法求证a>0,b>0,c>0的假设为( 2020-06-05 …
1,P(A)=0.4P(AB)=0.2P(A|B)+P(A非|B非)=1求P(A并B)2,证明若P 2020-06-14 …
b>0”的充要条件是“a+b>0,ab>o”试证“a>0,b>0”的充要条件是“a+b>0,ab> 2020-06-23 …
画图:①利用单位圆寻找适合下列条件的0°到360°的角1°sinα≥122°tanα>33②求证: 2020-07-18 …
请用反证法证明,若0 2020-08-01 …
已知a+b+c>0,ab+bc+ac>0,abc>0,用反证法求证a>0,b>0,c>0的假设为( 2020-08-01 …
已知函数f(x)=x(2+a丨x丨),且关于x的不等式f(x+a)<f(x)的解集为A,若[-0.5 2020-12-08 …