早教吧作业答案频道 -->数学-->
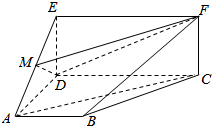
在如图所示的多面体中,四边形ABCD是梯形,∠BAD=∠CDA=90°,四边形CDEF是矩形,平面ABCD⊥平面CDEF,AB=AD=DE=12CD=2,M是线段AE的中点.(I)求证:AC∥平面MDF;(Ⅱ)平面MDF将该几何体分成两部
题目详情
在如图所示的多面体中,四边形ABCD是梯形,∠BAD=∠CDA=90°,四边形CDEF是矩形,平面ABCD⊥平面CDEF,AB=AD=DE=
CD=2,M是线段AE的中点.
(I)求证:AC∥平面MDF;
(Ⅱ)平面MDF将该几何体分成两部分,求多面体MDFE和多面体ABCDMF的体积之比.
| 1 |
| 2 |
(I)求证:AC∥平面MDF;
(Ⅱ)平面MDF将该几何体分成两部分,求多面体MDFE和多面体ABCDMF的体积之比.

▼优质解答
答案和解析
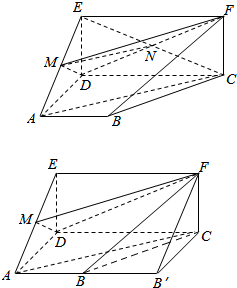 (I)证明:连结CE,交DF于N,连结MN,
(I)证明:连结CE,交DF于N,连结MN,
由题意知N为CE的中点,
在△ACE中,MN∥AC,…(3分)
且MN⊂面MDF,AC⊈平面MDF,
∴AC∥平面MDF.…(6分)
(II) 将多面体ABCDEF补成三棱柱ADE-B'CF,如图,
则三棱柱的体积为:
V=S△ADE•CD=
×2×2×4=8,…(8分)
而三棱锥F-DEM的体积VM-DEF=
,
则V多面体ABCDMF=V-VF-BB‘C-VM-DEF=8-
-
=
,
∴多面体MDFE和多面体ABCDMF的体积之比为
=
.…(12分)
 (I)证明:连结CE,交DF于N,连结MN,
(I)证明:连结CE,交DF于N,连结MN,由题意知N为CE的中点,
在△ACE中,MN∥AC,…(3分)
且MN⊂面MDF,AC⊈平面MDF,
∴AC∥平面MDF.…(6分)
(II) 将多面体ABCDEF补成三棱柱ADE-B'CF,如图,
则三棱柱的体积为:
V=S△ADE•CD=
| 1 |
| 2 |
而三棱锥F-DEM的体积VM-DEF=
| 4 |
| 3 |
则V多面体ABCDMF=V-VF-BB‘C-VM-DEF=8-
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
∴多面体MDFE和多面体ABCDMF的体积之比为
| VM-DEF |
| VABCDEF |
| 1 |
| 4 |
看了在如图所示的多面体中,四边形A...的网友还看了以下:
初二全等形数学题、、、、如图所示.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D, 2020-04-27 …
下列条件不能判定△ABC≌△DEF的是( )A. AB=DE、AC=DF、BC=EFB. AB= 2020-05-13 …
如图,在四边形ABCD中,∠B=∠D,AB=CD,BF=DE,AD=BC,求证:四边形AFCE是平 2020-05-17 …
表达式“Y=(A-B/C)×(D+E)”的后缀式表示为(29)。A.YAB-/C×DE+=B.YAB 2020-05-26 …
在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE 2020-07-25 …
如图在四边形ABCD中,角B=∠D=90角a比角c=1比2AB=2CD=1四边形ABCD是一个直角 2020-08-01 …
把下列解题补充完整:如图,已知:AB∥DE,∠B=80°,∠D=140°,求∠BCD的度数.如解题 2020-08-01 …
已知三角形ABC为等边三角形,点D为BC边上任意一点,角ADE等于60度,边DE与角ACB的外角平 2020-08-03 …
如图,已知点D在三角形ABC边BC上,且与B,D不重合,AC‖DE,AB‖DF,BC=5.1求证明 2020-08-03 …
如图,△ABC中,∠C=90°,D为AB中点,E、F分别在AC、BC上,且DE⊥DF.求证:AE?= 2020-11-02 …