早教吧作业答案频道 -->数学-->
一块三角形材料如图所示,∠A=∠B=60°,用这块材料剪出一个矩形DEFG,其中,点D,E分别在边AB,AC上,点F,G在边BC上.设DE=x,矩形DEFG的面积s与x之间的函数解析式是s=-
题目详情
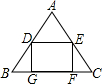
一块三角形材料如图所示,∠A=∠B=60°,用这块材料剪出一个矩形DEFG,其中,点D,E分别在边AB,AC上,点F,G在边BC上.设DE=x,矩形DEFG的面积s与x之间的函数解析式是s=-
x2+
x,则AC的长是___.
| ||
| 2 |
| | 3 |

▼优质解答
答案和解析
∵∠A=∠B=60°,
∴∠A=∠B=∠C,
∴△ABC是等边三角形,
∴BC=AC,
∵DE=x,
∴DE、GF之间的距离=
(BC-x)=
(AC-x),
∴矩形DEFG的面积s=
(AC-x)x=-
x2+
AC•x,
又∵s与x之间的函数解析式是s=-
x2+
x,
∴AC=2.
故答案为:2.
∴∠A=∠B=∠C,
∴△ABC是等边三角形,
∴BC=AC,
∵DE=x,
∴DE、GF之间的距离=
| ||
| 2 |
| ||
| 2 |
∴矩形DEFG的面积s=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
又∵s与x之间的函数解析式是s=-
| ||
| 2 |
| 3 |
∴AC=2.
故答案为:2.
看了一块三角形材料如图所示,∠A=...的网友还看了以下:
AC平分角BAD,CD垂直AD于D,CB垂直AB于B,E是AC上一点,求证角AED=角AEBAC平分 2020-03-30 …
AC平分∠BAD,CD⊥AD于点D,CB⊥AB于B,E是AC上一点.求证∠AED=∠AEB 2020-03-30 …
最好有图片,不要直接答案如图12-11,在梯形ABCD中,AD∥BC,∠C=90°,AD=b,BC= 2020-03-30 …
如果两个相似三角形对应高的比为5比4,对应中线的比为?对应叫平分线的比?若三角形ABC与三角形A' 2020-06-02 …
在长方形abcd中AB=a,AD=b,E是AD边上一点,AE:AD=n1·当n=----时,S△d 2020-06-08 …
在长方形abcd中AB=a,AD=b,E是AD边上一点,AE:AD=n1·当n=----时,S△d 2020-06-08 …
如图,在三角形ABC中,点D.E在边BC上,角CAE=角B,E是CD的中点,且AD平分角BAE.1 2020-06-08 …
化学有毒气体A.D是两种常见的固体,其中D为亮红色;B.E是两种常见的气体,其中气体E有剧毒,他们 2020-07-11 …
泰历中年份前面的B.E.是什么意思?比如:21JuneB.E.2552 2020-07-23 …
若函数f(x)在其定义域内某一区间[a,b]e连续,且对[a,b]中任意实数x地,x2,都有f(x 2020-07-29 …