早教吧作业答案频道 -->数学-->
如图,已知多面体A-BCDEF中,ABCD为菱形,∠ABC=60°,AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥BE.(I)求证:AF⊥平面BDE;(Ⅱ)求多面体ABCDEF的体积.
题目详情
如图,已知多面体A-BCDEF中,ABCD为菱形,∠ABC=60°,AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥BE.
(I)求证:AF⊥平面BDE;
(Ⅱ)求多面体ABCDEF的体积.
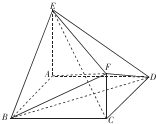
(I)求证:AF⊥平面BDE;
(Ⅱ)求多面体ABCDEF的体积.

▼优质解答
答案和解析
(Ⅰ)证明:连AC交BD于O,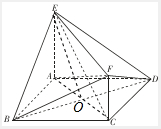
∵四边形ABCD是菱形,∴BD⊥AC,
∵AE⊥面ABCD,BD⊂面ABCD,
∴BD⊥AE,又∵AC⊂平面ACE,AE⊂平面ACE,AC∩AE=A,
∴BD⊥面EACF,∵AF⊂面EACF,
∴BD⊥AF.又AF⊥BE,BD⊂平面BDE,BE⊂平面BDE,BD∩BE=B,
∴AF⊥面BDE.
(Ⅱ) 连结OE,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=AE=1,OB=OD=
.
∵AF⊥面BDE,EO⊂面BDE,
∴EO⊥AF,
∴∠AEO=90°-∠EAF,∠CAF=90°-∠EAF,
∴∠AEO=∠CAF.
∵tan∠AEO=
=
,∴tan∠CAF=
=
∴FC=
,
∴VB-ACFE=
S梯形ACFE•BO=
×
×(1+
)×1×
=
.
设所求多面体的体积V=2VB-ACFE=
.

∵四边形ABCD是菱形,∴BD⊥AC,
∵AE⊥面ABCD,BD⊂面ABCD,
∴BD⊥AE,又∵AC⊂平面ACE,AE⊂平面ACE,AC∩AE=A,
∴BD⊥面EACF,∵AF⊂面EACF,
∴BD⊥AF.又AF⊥BE,BD⊂平面BDE,BE⊂平面BDE,BD∩BE=B,
∴AF⊥面BDE.
(Ⅱ) 连结OE,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=AE=1,OB=OD=
| ||
| 2 |
∵AF⊥面BDE,EO⊂面BDE,
∴EO⊥AF,
∴∠AEO=90°-∠EAF,∠CAF=90°-∠EAF,
∴∠AEO=∠CAF.
∵tan∠AEO=
| AO |
| AE |
| 1 |
| 2 |
| CF |
| AC |
| 1 |
| 2 |
∴FC=
| 1 |
| 2 |
∴VB-ACFE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
设所求多面体的体积V=2VB-ACFE=
| ||
| 4 |
看了如图,已知多面体A-BCDEF...的网友还看了以下:
读如图两幅图,完成图后填空.(1)A、B、C三点都位于地球上五带中的带,一年中太阳直射两次光临点. 2020-04-09 …
如图是人体受到寒冷刺激时,内分泌腺活动的调节示意图.请据图回答:(1)下丘脑内神经元(A与B)之间 2020-05-15 …
如图四、已知数轴上A、B、C、D四点,对应的实数都是整数,如果A对应的实数为a、B为b、且b-2a 2020-05-15 …
如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A、B、C、D路线运动, 2020-05-16 …
已知a,b,c成等比数列,如果a,x,b和b,y,c都成等差数列,则a/x + c/y=?下面是某 2020-05-16 …
如图正方形被一条曲线分成A、B两部分,下面()说法正确.A.如果a>b,那么A周长大于B周长B.如 2020-05-17 …
如图,水平面上叠放着a、b两木块,用手轻推木块b,a会跟着一起运动;若用锤子水平猛击一下b,a就不 2020-06-19 …
如图所示,A与B两滑块叠放在水平面上,已知A与B所受重力分别为GA=10N,GB=20N,A与B间 2020-07-07 …
如图,已知圆心为A,B,C的三个圆彼此相切,且均与直线l相切.若⊙A,⊙B,⊙C的半径分别为a,b 2020-07-31 …
有下列四个命题:1.若a、b是不相等的无理数,则ab+a-b是无理数2.若a、b是不相等的无理数, 2020-08-01 …