早教吧作业答案频道 -->数学-->
已知在平面直角坐标系中,点A(1,2),点B(4,1),点C(-3,-2).(1)在x轴上找一点D,使AD+BD最小,求点D坐标;(2)在y轴上找一点E,使|AE-CE|最大,求点E坐标.
题目详情
已知在平面直角坐标系中,点A(1,2),点B(4,1),点C(-3,-2).
(1)在x轴上找一点D,使AD+BD最小,求点D坐标;
(2)在y轴上找一点E,使|AE-CE|最大,求点E坐标.
(1)在x轴上找一点D,使AD+BD最小,求点D坐标;
(2)在y轴上找一点E,使|AE-CE|最大,求点E坐标.
▼优质解答
答案和解析
如图所示:
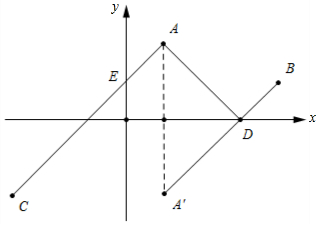
(1)点A(1,2)关于x轴的对称点为A'(1,-2),连接A'B交x轴于点D,
设直线A'B的解析式为y=kx+b,
将A'和B点的坐标代入可得
,解得
,
∴A'B的解析式为y=x-3,
∴D点的坐标为(3,0);
(2)∵|AE-CE|≤AC,当AEC三点共线时|AE-CE|最大,
∴连接AC交于点E,点E即为所求,
设AC的解析式为y=mx+n,
将A、C两点坐标代入可得
,解得
,
∴AC的解析式为y=x+1,
∴E点的坐标为(0,1).

(1)点A(1,2)关于x轴的对称点为A'(1,-2),连接A'B交x轴于点D,
设直线A'B的解析式为y=kx+b,
将A'和B点的坐标代入可得
|
|
∴A'B的解析式为y=x-3,
∴D点的坐标为(3,0);
(2)∵|AE-CE|≤AC,当AEC三点共线时|AE-CE|最大,
∴连接AC交于点E,点E即为所求,
设AC的解析式为y=mx+n,
将A、C两点坐标代入可得
|
|
∴AC的解析式为y=x+1,
∴E点的坐标为(0,1).
看了已知在平面直角坐标系中,点A(...的网友还看了以下:
ABD.ABC为两个光滑固定轨道,A.B.E在同一水平线上,C.D.E在同一竖直线上D点拒水平面的 2020-05-24 …
如图,在△ABC中,AB=AC,cosB=1/3,BC=2,点D,E,F分别在AC,AB,BC边上 2020-06-27 …
如图,在矩形ABCD中,E为CD上一点,将△ADE沿直线AE翻折,使点D落在BC边上点D′处(1) 2020-07-20 …
已知三角形ABC中,AB=AC,D,E在三角形ABC中,AB=AC,点D,E是BC边上的点,将三角 2020-07-21 …
1.在RtA△BC中,∠C=90°.D,E分别是AB,AC的中点,AC=7,BC=4,若以C为圆心 2020-07-26 …
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E 2020-07-31 …
直线a,b是异面直线,A,B,C为直线a上三点,D,E,F是直线b上三点,A',B',C',D', 2020-07-31 …
求面面夹角的公式已知空间坐标中6个点A.B.C.D.E.F.坐标分别为(x1,y1,z1).(x6 2020-07-31 …
等边三角形ABC边长是6,点D,E风别在AB,AC上,且AD=AE=2已知△ABC是边长为6的等边 2020-08-03 …
如图,点O是线段AB的中点,点C在线段AO上,点D在线段OB上,E,F是线段AB上任意两点如图,点O 2020-12-06 …