早教吧作业答案频道 -->数学-->
如图1,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数y=-x2的图象为l1.(1)平移抛物线l1,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个
题目详情
如图1,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数y=-x2的图象为l1.
(1)平移抛物线l1,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可);
(2)平移抛物线l1,使平移后的抛物线过A、B两点,记抛物线为l2,如图2,求抛物线l2的函数解析式及顶点C的坐标;
(3)设P为y轴上一点,且S△ABC=S△ABP,求点P的坐标;
(4)请在图2上用尺规作图的方式探究抛物线l2上是否存在点Q,使△QAB为等腰三角形?若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.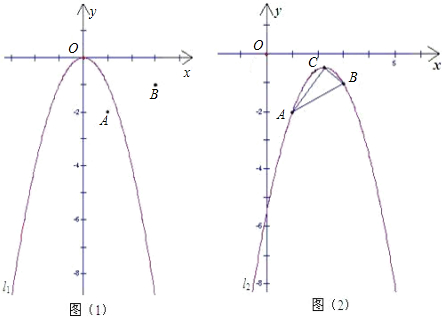
(1)平移抛物线l1,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可);
(2)平移抛物线l1,使平移后的抛物线过A、B两点,记抛物线为l2,如图2,求抛物线l2的函数解析式及顶点C的坐标;
(3)设P为y轴上一点,且S△ABC=S△ABP,求点P的坐标;
(4)请在图2上用尺规作图的方式探究抛物线l2上是否存在点Q,使△QAB为等腰三角形?若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.

▼优质解答
答案和解析
(1)让抛物线过点A,即把点A的坐标代入计算,得到,b+c=-1,不过点B,则把点B的坐标代入得到3b+c≠8,依此两个要求,随便找一个数即可.故平移后的抛物线的一个解析式y=-x2+2x-3或y=-x2+4x-5等(满足条件即可);(1分)
(2)设l2的解析式为y=-x2+bx+c,联立方程组
,
解得:b=
,c=-
,则l2的解析式为y=-x2+
x-
.(3分)
点C的坐标为(
,-
).(4分)
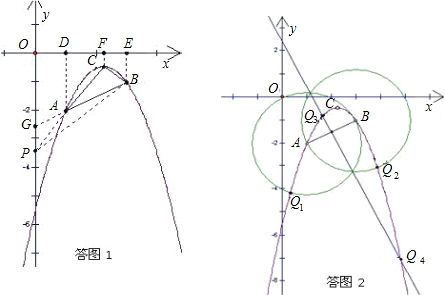
(3)如答图1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,
则AD=2,CF=
,BE=1,DE=2,DF=
,FE=
.
得:S△ABC=S梯形ABED-S梯形BCFE-S梯形ACFD=
.(5分)
延长BA交y轴于点G,直线AB的解析式为y=
x-
,则点G的坐标为(0,-
),设点P的坐标为(0,h),
①当点P位于点G的下方时,PG=-
-h,连接AP、BP,
则S△ABP=S△BPG-S△APG=-
-h,又S△ABC=S△ABP=
,得h=-
,点P的坐标为(0,-
).(6分)
②当点P位于点G的上方时,PG=
+h,同理h=-
,点P的坐标为(0,-
).
综上所述所求点P的坐标为(0,-
)或(0,-
)(7分)
(4)作图痕迹如答图2所示.
若AB为等腰三角形的腰,则分别以A、B为圆心,以AB长为半径画�

(2)设l2的解析式为y=-x2+bx+c,联立方程组
|
解得:b=
| 9 |
| 2 |
| 11 |
| 2 |
| 9 |
| 2 |
| 11 |
| 2 |
点C的坐标为(
| 9 |
| 4 |
| 7 |
| 16 |
(3)如答图1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,
则AD=2,CF=
| 7 |
| 16 |
| 5 |
| 4 |
| 3 |
| 4 |
得:S△ABC=S梯形ABED-S梯形BCFE-S梯形ACFD=
| 15 |
| 16 |
延长BA交y轴于点G,直线AB的解析式为y=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
①当点P位于点G的下方时,PG=-
| 5 |
| 2 |
则S△ABP=S△BPG-S△APG=-
| 5 |
| 2 |
| 15 |
| 16 |
| 55 |
| 16 |
| 55 |
| 16 |
②当点P位于点G的上方时,PG=
| 5 |
| 2 |
| 25 |
| 16 |
| 25 |
| 16 |
综上所述所求点P的坐标为(0,-
| 55 |
| 16 |
| 25 |
| 16 |
(4)作图痕迹如答图2所示.
若AB为等腰三角形的腰,则分别以A、B为圆心,以AB长为半径画�
看了如图1,在平面直角坐标系中,点...的网友还看了以下:
如图,矩形OABC,OA=9,AB=15,点E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处 2020-04-07 …
如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点 2020-04-13 …
如图1,2,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶 2020-04-13 …
如图(1),(2),四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D, 2020-04-13 …
如图所示,一薄壁导体球壳(以下简称为球壳)的球心在O点.球壳通过一细导线与端电压U=90V的电池的 2020-05-16 …
椭圆:16,已知椭圆C的中心在原点,一个焦点为F(-2,0),且长轴与短轴长的比是2:√3.(2) 2020-05-16 …
(2009•闸北区二模)如图,AB是山顶一铁塔,C是地面上一点.若已知塔高为h,在A处测得C点的俯 2020-05-17 …
真空中有一个电荷量为+Q的点电荷,固定在A点.在与A点相距为r的B点,电场强度大小为kQr2kQr 2020-06-12 …
如图,在梯形ABCD中,AD∥BC,AB=DC=AD=9,∠ABC=70°,点E,F分别在线段AD 2020-06-13 …
在平面直角坐标系中,A为x轴负半轴上一点.B为x轴上一点,C(0,-2),D(-3,-2),直线M 2020-06-13 …