早教吧作业答案频道 -->数学-->
定理表述请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述);尝试证明以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请
题目详情
【定理表述】
请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述);
【尝试证明】
以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;
【知识拓展】
利用图2中的直角梯形,我们可以证明
<
.其证明步骤如下:
∵BC=a+b,AD=___.
又∵在直角梯形ABCD中有BC___AD(填大小关系),即___,
∴
<
.
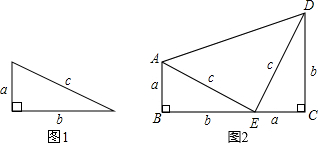
请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述);
【尝试证明】
以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;
【知识拓展】
利用图2中的直角梯形,我们可以证明
| a+b |
| c |
| | 2 |
∵BC=a+b,AD=___.
又∵在直角梯形ABCD中有BC___AD(填大小关系),即___,
∴
| a+b |
| c |
| | 2 |

▼优质解答
答案和解析
【定理表述】如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2.
【尝试证明】
∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED,
∴
(a+b)(a+b)=
ab+
ab+
c2,
整理,得a2+b2=c2.
【知识拓展】
∵AD=
c,BC<AD,
∴a+b<
c,即
<
,
故答案为:
c,<,a+b<
c
【尝试证明】
∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理,得a2+b2=c2.
【知识拓展】
∵AD=
| 2 |
∴a+b<
| 2 |
| a+b |
| c |
| 2 |
故答案为:
| 2 |
| 2 |
看了定理表述请你根据图1中的直角三...的网友还看了以下:
已知角A=125°-a,角B=a-35°,则角A与角B的关系是什么A、互补B、互余C、相等D、角A 2020-04-09 …
在三角形abc中,a.b分别是角A和角B.a=根号3,b=1,B为30度,求角A? 2020-04-27 …
已知三角形ABC与三角形A'B'C'中,AB=A'B',BC=B'C',角BAC=角B'C'A'= 2020-05-16 …
设A、B、C为三角形的三内角,且方程(sinB-sinA)x2+(sinA-sinC)x +(si 2020-05-16 …
△ABC中,AB=4,AC=42,∠BAC=45°,以AC的中线BD为折痕,将△ABD沿BD折起, 2020-06-27 …
如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在 2020-07-04 …
如图,下列说法错误的是()A.∠A与∠EDC是同位角B.∠A与∠ABF是内错角C.∠A与∠ADC是 2020-07-23 …
如图所示,下列说法错误的是()A.∠A和∠B是同旁内角B.∠A和∠3是内错角C.∠1和∠3是内错角 2020-07-23 …
VB中已知A角与B角,B-A得出C角,求tan-1(C),如何实现.本人vb初学者, 2020-11-15 …
对于任意的两个数AB,规定新的运算,a三角B=A*(a+1)*(A+2)*·····*(A+B-1) 2020-12-01 …