早教吧作业答案频道 -->数学-->
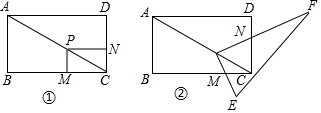
探究:如图①,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,过点P分别作AB、AD的平行线,交BC、CD于点M、N,求PMPN的值;应用:如图②,在矩形ABCD中,AB=3,AD=4,点P
题目详情
探究:如图①,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,过点P分别作AB、AD的平行线,交BC、CD于点M、N,求
的值;
应用:如图②,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,Rt△PEF的两条直角边PE、PF分别交BC、CD于点M、N,则
=___.
| PM |
| PN |
应用:如图②,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,Rt△PEF的两条直角边PE、PF分别交BC、CD于点M、N,则
| PM |
| PN |

▼优质解答
答案和解析
探究: 如图①中,
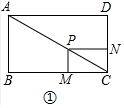
∵四边形ABCD是矩形,
∴∠B=∠DCB=90°,AD=BC=4,
∵PM⊥BC,PN⊥CD,
∴∠PMC=∠PNC=90°,
∴四边形PMCN是矩形,
∴PC=CM,
∵∠PMC=∠B=90°,
∴PM∥AB,
∴△CPM∽△CAB,
∴
=
,即
=
,
∵AB=3,BC=4
∴
=
=
=
.
应用: 如图②中,过P作PG⊥BC于G,作PH⊥CD于H,则∠PGM=∠PHN=90°,∠GPH=90°,
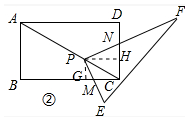
∵Rt△PEF中,∠FPE=90°
∴∠GPM=∠HPN
∴△PGM∽△PHN
∴
=
,
由条件可知,
=
=
,
∴
=
.
故答案为
.

∵四边形ABCD是矩形,
∴∠B=∠DCB=90°,AD=BC=4,
∵PM⊥BC,PN⊥CD,
∴∠PMC=∠PNC=90°,
∴四边形PMCN是矩形,
∴PC=CM,
∵∠PMC=∠B=90°,
∴PM∥AB,
∴△CPM∽△CAB,
∴
| PM |
| AB |
| CM |
| CB |
| PM |
| CM |
| AB |
| BC |
∵AB=3,BC=4
∴
| PM |
| PN |
| PM |
| CM |
| AB |
| BC |
| 3 |
| 4 |
应用: 如图②中,过P作PG⊥BC于G,作PH⊥CD于H,则∠PGM=∠PHN=90°,∠GPH=90°,

∵Rt△PEF中,∠FPE=90°
∴∠GPM=∠HPN
∴△PGM∽△PHN
∴
| PM |
| PN |
| PG |
| PH |
由条件可知,
| PG |
| PH |
| AB |
| BC |
| 3 |
| 4 |
∴
| PM |
| PN |
| 3 |
| 4 |
故答案为
| 3 |
| 4 |
看了探究:如图①,在矩形ABCD中...的网友还看了以下:
矩形ABCD,AD=10,AB=4,将一个足够大的直角三角形PHF的直角顶点P落在AD上,(P点可 2020-05-15 …
在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边PQ在BC上,EF俩点分别在 2020-06-07 …
若从矩形一边上的点到对边的视角是直角,则称该点为直角点.例如,如图的矩形ABCD中,点M在CD边上 2020-06-17 …
如图,矩形ABCD中,AB=4,AD=16,点o是矩形ABCD内一点,且点O到三边AB,BC与AD 2020-06-25 …
小学的时候课本上是说闰年是4年一次吧?但是现在有个问题困扰了.说要计算某年是不是闰年是用年份除4. 2020-07-10 …
如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△C 2020-07-30 …
如图,将一张矩形纸片沿它的长边对折(EF为折痕),得到两个全等的小如图,将一张矩形纸片沿它的长边对 2020-07-31 …
不要复制的,不要发图片答案,我用的是手机看不到!如图,四棱锥P-ABCD中,PD⊥平面ABCD,底 2020-08-01 …
小方与朋友约好,下午4点30在咖啡厅见面,为此他们在早上8点钟没人均将自己的表对准,小方于4点30正 2020-11-07 …
如图,四边形ABCD为矩形,C点在x轴上,A点在y轴上,D点坐标是(0,0),B点坐标是(3,4), 2020-12-25 …