早教吧作业答案频道 -->数学-->
如图,Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB的外角平分线CF相交于点D,AD交CB于P,CF交AB的延长线于F,过D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长线交FG于点H
题目详情
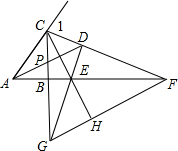
如图,Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB的外角平分线CF相交于点D,AD交CB于P,CF交AB的延长线于F,过D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长线交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG,其中正确的有___.

▼优质解答
答案和解析
①利用公式:∠CDA=
∠ABC=45°,①正确;
②如图:延长GD与AC交于点P,
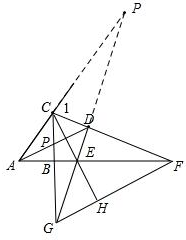
由三线合一可知CG=CP,
∵∠ADC=45°,DG⊥CF,
∴∠EDA=∠CDA=45°,
∴∠ADP=∠ADF,
∴△ADP≌△ADF(ASA),
∴AF=AP=AC+CP=AC+CG,故②正确;
③如图:
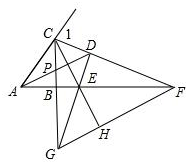
∵∠EDA=∠CDA,
∠CAD=∠EAD,
从而△CAD≌△EAD,
故DC=DE,③正确;
④∵BF⊥CG,GD⊥CF,
∴E为△CGF垂心,
∴CH⊥GF,且△CDE、△CHF、△GHE均为等腰直角三角形,
∴HF=CH=EH+CE=GH+CE=GH+
CD,故④错误;
⑤如图:作ME⊥CE交CF于点M,
则△CEM为等腰直角三角形,从而CD=DM,CM=2CD,EM=EC,
∵∠MFE=∠CGE,
∠CEG=∠EMF=135°,
∴△EMF≌△CEG(AAS),
∴GE=MF,
∴CF=CM+MF=2CD+GE,
故⑤正确;
综上所述,
答案为:①②③⑤.
| 1 |
| 2 |
②如图:延长GD与AC交于点P,

由三线合一可知CG=CP,
∵∠ADC=45°,DG⊥CF,
∴∠EDA=∠CDA=45°,
∴∠ADP=∠ADF,
∴△ADP≌△ADF(ASA),
∴AF=AP=AC+CP=AC+CG,故②正确;
③如图:

∵∠EDA=∠CDA,
∠CAD=∠EAD,
从而△CAD≌△EAD,
故DC=DE,③正确;
④∵BF⊥CG,GD⊥CF,
∴E为△CGF垂心,
∴CH⊥GF,且△CDE、△CHF、△GHE均为等腰直角三角形,
∴HF=CH=EH+CE=GH+CE=GH+
| 2 |
⑤如图:作ME⊥CE交CF于点M,
则△CEM为等腰直角三角形,从而CD=DM,CM=2CD,EM=EC,
∵∠MFE=∠CGE,
∠CEG=∠EMF=135°,
∴△EMF≌△CEG(AAS),
∴GE=MF,
∴CF=CM+MF=2CD+GE,
故⑤正确;
综上所述,
答案为:①②③⑤.
看了如图,Rt△ABC中,∠CBA...的网友还看了以下:
如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P 2020-05-02 …
在平面直角坐标系中,已知抛物线y=-x的平方+bx+c与x轴交于点A、B(点A在点B的左侧),与y 2020-05-16 …
已知二次函数y=ax2+bx+c的图像与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正已知 2020-05-16 …
如图,在平面直角坐标系xoy中,抛物线y=x2+bx+c与x轴交于a、b两点(点a在点b的左侧), 2020-05-16 …
在平面直角坐标系x0y中,抛物线y=x2+bx+c与X轴交于A、B两点(点A在点B的左侧)与Y轴交 2020-05-16 …
抛物线y=x2+bx+c(b≤0)的图像与x轴交于A,B两点,与y轴交于点C,其中点A的坐标为(- 2020-06-03 …
已知:如图,在平面直角坐标系中,直线AB与x轴和y轴分别交于A、B两点,与直线OC交于点C,点C的 2020-06-14 …
如图已知抛物线Y=1/2X+bx+C经过点A(4,0)和点(0,4),交X轴于点C,过OB的中点, 2020-06-14 …
如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关 2020-07-09 …
(2014?潍坊)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A 2020-11-13 …