早教吧作业答案频道 -->数学-->
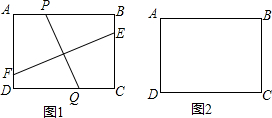
如图,在长方形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.线段PQ的垂直平分线与直线BC、AD分别相交与点E、F点.(1)若E、F分
题目详情
如图,在长方形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.线段PQ的垂直平分线与直线BC、AD分别相交与点E、F点.
(1)若E、F分别与B、D重合,求AP的长.
(2)当E、F在边BC、AD上时,设AP=x,BE=y,求y与x的函数关系式及x取值范围;
(3)是否存在这样的一点P,使△PQE为直角三角形?若存在,请求出AP的值,若不存在请说明理由.
(1)若E、F分别与B、D重合,求AP的长.
(2)当E、F在边BC、AD上时,设AP=x,BE=y,求y与x的函数关系式及x取值范围;
(3)是否存在这样的一点P,使△PQE为直角三角形?若存在,请求出AP的值,若不存在请说明理由.

▼优质解答
答案和解析
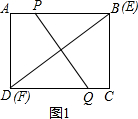 (1)如图1,AP=x,则BP=8-x;
(1)如图1,AP=x,则BP=8-x;
∵BD垂直平分PQ;
∴PB=BQ=8-x
Rt△BQC中
(8-x)2=x2+62,
解得:x=
,则AP=
;
(2)连接EP、EQ
∵EF垂直平分PQ;
∴EP=EQ
在Rt△PBE和Rt△QCE中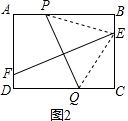
(8-x)2+y2=x2+(6-y)2,
则y=
,
∵0≤y≤6,
∴
≤x≤
;
(3)当E在BC边上,若△PQE为直角三角形,则只有∠PEQ=90°,
∵∠PEQ=90°,
∴∠PEB+∠QEC=90°,
∵∠BPE+∠PEB=90°,
∴∠BPE=∠QEC,
在△PBE和△ECQ中
∵
,
∴△PBE≌△ECQ(AAS),
则BE=CQ=x=y,
∵y=
,
∴解得:x=7,
∵x=7不在定义域范围内,
∴不存在,
当E在边BC(或CB)延长线上时,△PQE每个角都小于90°,不可能为直角三角形,
综上所述,这样的P点不存在.
 (1)如图1,AP=x,则BP=8-x;
(1)如图1,AP=x,则BP=8-x;∵BD垂直平分PQ;
∴PB=BQ=8-x
Rt△BQC中
(8-x)2=x2+62,
解得:x=
| 7 |
| 4 |
| 7 |
| 4 |
(2)连接EP、EQ
∵EF垂直平分PQ;
∴EP=EQ
在Rt△PBE和Rt△QCE中

(8-x)2+y2=x2+(6-y)2,
则y=
| 4x-7 |
| 3 |
∵0≤y≤6,
∴
| 7 |
| 4 |
| 25 |
| 4 |
(3)当E在BC边上,若△PQE为直角三角形,则只有∠PEQ=90°,
∵∠PEQ=90°,
∴∠PEB+∠QEC=90°,
∵∠BPE+∠PEB=90°,
∴∠BPE=∠QEC,
在△PBE和△ECQ中
∵
|
∴△PBE≌△ECQ(AAS),
则BE=CQ=x=y,
∵y=
| 4x-7 |
| 3 |
∴解得:x=7,
∵x=7不在定义域范围内,
∴不存在,
当E在边BC(或CB)延长线上时,△PQE每个角都小于90°,不可能为直角三角形,
综上所述,这样的P点不存在.
看了如图,在长方形ABCD中,AB...的网友还看了以下:
点A,B,C,D分别是蛋圆与坐标轴的焦点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心 2020-04-26 …
直线m交x轴 y轴与点A B 与反比例函数的图像交于C D两点、直线m交x轴 y轴与点A B 与反 2020-05-16 …
如图1,将一张对边平行的纸条沿ef折叠,点a,b分别落在a',b'处,线段fb'与ad交与点m.1 2020-06-02 …
八下数学补充习题的一题:已知反比例函数y=x分之k的图像经过点P(-2,-3)(1)画出该图像经过 2020-07-13 …
若b分之a=c分之b=d分之c=a分之d,则a+b-c+d分之a-b+c-d 2020-07-29 …
已知直线a.b是异面直线,直线c.d分别与ab都相交,求直线cd的位置关系()a.可能已知直线a. 2020-08-02 …
在创建卫生城市活动中,某小区居民全员参与共建文明小区.居民举止与社区文明的关系突出体现的哲学原理是A 2020-11-27 …
直线a,b,c,d交一点P,且a,b,c,d都与直线l相交,交点分别为A,B,C,D,求证a,b,c 2020-11-27 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
直线c,d分别与直线a,b相交,∠1与∠2互余,∠1与∠3互补,试说明直线c,d互相垂直 2020-12-01 …