早教吧作业答案频道 -->数学-->
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.(1)如图1,若α=60°,点P与点M重合,则∠BDA=
题目详情
在△ABC中,AB=AC,∠ACB=α,点M是BC的中点,点P是线段AM上的动点,将线段PC绕点P顺时针旋转2α得到线段PQ,线段BQ的延长线交AM延长线于点D.
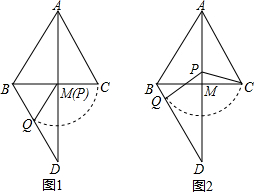
(1)如图1,若α=60°,点P与点M重合,则∠BDA=___;
(2)如图2,点P不与点A、点M重合,则∠BDA=___.(用含α的式子表示)

(1)如图1,若α=60°,点P与点M重合,则∠BDA=___;
(2)如图2,点P不与点A、点M重合,则∠BDA=___.(用含α的式子表示)
▼优质解答
答案和解析
(1)∵AB=AC,M是BC的中点,
∴AM⊥BC,
∴∠BMD=90°,
∵∠CMQ=2α=120°,
∴∠BMP=60°,
∵BM=MC=MQ,
∴∠MBQ=60°,
∴∠BDA=90°-60°=30°,
故答案为:30°;
(2)如图,连接PB,CD,
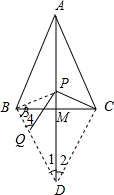
∵AC=AB,M是BC的中点,
∴AM⊥BC,
即AD为BC的垂直平分线,
∴BD=CD,BP=PC,PD=PD,
在△BPD与△CPD中,
,
∴△BPD≌△CPD(SSS),
∴∠CDA=∠BDA,∠PBD=∠PCD,
又∵PQ=PC,
∴PQ=PB,∠BDC=2∠1,∠4=∠PBQ=∠PCD,
∴∠PCD+∠PQD=∠4+∠PQD=180°,
∴∠CPQ+∠BDC=360°-(∠PCD+∠PQD)=180°,
∴∠BDA=180°-∠CPQ=180°-2α,
∴2∠BDA=180°-2α,
∴∠BDA=90°-α.
故答案为:90°-α.
∴AM⊥BC,
∴∠BMD=90°,
∵∠CMQ=2α=120°,
∴∠BMP=60°,
∵BM=MC=MQ,
∴∠MBQ=60°,
∴∠BDA=90°-60°=30°,
故答案为:30°;
(2)如图,连接PB,CD,

∵AC=AB,M是BC的中点,
∴AM⊥BC,
即AD为BC的垂直平分线,
∴BD=CD,BP=PC,PD=PD,
在△BPD与△CPD中,
|
∴△BPD≌△CPD(SSS),
∴∠CDA=∠BDA,∠PBD=∠PCD,
又∵PQ=PC,
∴PQ=PB,∠BDC=2∠1,∠4=∠PBQ=∠PCD,
∴∠PCD+∠PQD=∠4+∠PQD=180°,
∴∠CPQ+∠BDC=360°-(∠PCD+∠PQD)=180°,
∴∠BDA=180°-∠CPQ=180°-2α,
∴2∠BDA=180°-2α,
∴∠BDA=90°-α.
故答案为:90°-α.
看了在△ABC中,AB=AC,∠A...的网友还看了以下:
若将数轴折叠,使得A点与-3表示的点重合,则B点与数()表示的点重合若数轴上M、N两点之间的距离为 2020-05-13 …
已知反比例函数y=kx与直线y=1/4x相交于A.B两点.第一象限上M(m,n)已知双曲线y=k/ 2020-05-13 …
二次函数E(3,0)为圆心以5为半径的园E与X轴交于C点,抛物线Y=aX²+bX+c经过A,B,C 2020-05-13 …
A,B为空间的两个不同的点,且AB=1,空间中适合条件向量AM点乘向量AB=1的点M的集合是怎样一 2020-05-16 …
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC 2020-05-17 …
将边长为8的正方形ABCD折叠,是顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折 2020-05-17 …
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E交BC于F,边AB折叠后与BC边 2020-05-17 …
李老师从“淋浴龙头”受到启发.编了一个题目:在数轴上截取从0到3的对应线段AB,实数m对应AB上的 2020-06-07 …
在直角坐标系中,点A、B的坐标分别为(-2,4)、(-5,2),点M在x轴上,点N在y轴上.如果以 2020-06-13 …
如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处 2020-06-27 …