早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,使得△BPC是一个等腰三角形.(1)用尺规作图画出符合要求的点P.(保留作图痕迹,不要求写作法)(2)求出PA的长.
题目详情
如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,使得△BPC是一个等腰三角形.

(1)用尺规作图画出符合要求的点P.(保留作图痕迹,不要求写作法)
(2)求出PA的长.

(1)用尺规作图画出符合要求的点P.(保留作图痕迹,不要求写作法)
(2)求出PA的长.
▼优质解答
答案和解析
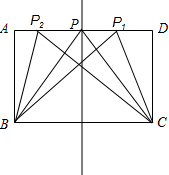 (1)如图所示:P,P1,P2即为所求;
(1)如图所示:P,P1,P2即为所求;
(2)当BC=BP1=6时,∵AB=4,
∴P1A=
=2
,
当CB=CP2=6时,P2A=AD-P2D=6-2
,
当PB=PC时,PA=
AD=3.
综上,PA的长为2
,6-2
,3.
 (1)如图所示:P,P1,P2即为所求;
(1)如图所示:P,P1,P2即为所求;(2)当BC=BP1=6时,∵AB=4,
∴P1A=
| 62-42 |
| 5 |
当CB=CP2=6时,P2A=AD-P2D=6-2
| 5 |
当PB=PC时,PA=
| 1 |
| 2 |
综上,PA的长为2
| 5 |
| 5 |
看了如图,在矩形ABCD中,AB=...的网友还看了以下:
1.已知 角AOB=90° OC是条射线,OM ON分别平分 角BOC和角AOC,请你根据不同情况 2020-05-16 …
已知抛物线Y=-X*2+4交X轴于A,B两点,顶点是C.1.求三角形ABC的面积.2若点P在Y=- 2020-06-14 …
如图.点E,F在BC上,BE等于CF,AB等于DC,角B等于角C.求证角A等于角C.根据概念(S如 2020-06-27 …
在直角坐标系中,已知A(a,0),B(0,b)(1)若a,b满足|2b+3a-17|+(b-a-1 2020-07-30 …
正弦定理求出角度,怎样取舍解三角形:b=8,c=3,A=60°求出a后,求得sinB=(4√3)/ 2020-08-02 …
怎样求三角形和梯形的斜边长?一个直角三角形的底边长10厘米,高是8厘米,怎样求三角形斜边的长?要求 2020-08-02 …
(2009•宿豫区模拟)已知三角形的三个顶点坐标,求三角形面积通常有以下三种方法:方法1:直接法. 2020-08-02 …
在RT三角形ABC中,角C=90度角B=30度BC=4左右平移等边三角形DEF的两个顶点E、F,始 2020-08-03 …
在三角形ABC中,AC=4,BC=3,角ACB=90度,D是AC边上一个动点(不与A、C重合),CE 2020-11-07 …
求如果求得的角的余弦值为负值的话,这说明两条异面直线所成的角应该是所求角的补角这句话是什么意思?在“ 2020-11-26 …