早教吧作业答案频道 -->数学-->
在数列{an}中,如果对任意的n∈N*,都有(λ为常数),则称数列{an}为比等差数列,λ称为比公差.则下列命题中真命题的序号是①若数列{Fn}满足F1=1,F2=1,Fn=Fn-1+Fn
题目详情
在数列{a n }中,如果对任意的n∈N * ,都有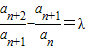 (λ为常数),则称数列{a n }为比等差数列,λ称为比公差.则下列命题中真命题的序号是
(λ为常数),则称数列{a n }为比等差数列,λ称为比公差.则下列命题中真命题的序号是
①若数列{F n }满足F 1 =1,F 2 =1,F n =F n-1 +F n-2 (n≥3),则该数列不是比等差数列;
②若数列{a n }满足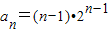 ,则数列{a n }是比等差数列,且比公差λ=2;
,则数列{a n }是比等差数列,且比公差λ=2;
③“等差数列是常数列”是“等差数列成为比等差数列”的充分必要条件;
④数列{a n }满足: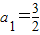 ,且
,且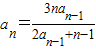 (n≥2,n∈N),则此数列的通项为
(n≥2,n∈N),则此数列的通项为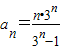 ,且{a n }不是比等差数列.
,且{a n }不是比等差数列.
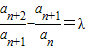 (λ为常数),则称数列{a n }为比等差数列,λ称为比公差.则下列命题中真命题的序号是
(λ为常数),则称数列{a n }为比等差数列,λ称为比公差.则下列命题中真命题的序号是 ①若数列{F n }满足F 1 =1,F 2 =1,F n =F n-1 +F n-2 (n≥3),则该数列不是比等差数列;
②若数列{a n }满足
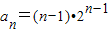 ,则数列{a n }是比等差数列,且比公差λ=2;
,则数列{a n }是比等差数列,且比公差λ=2;③“等差数列是常数列”是“等差数列成为比等差数列”的充分必要条件;
④数列{a n }满足:
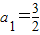 ,且
,且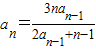 (n≥2,n∈N),则此数列的通项为
(n≥2,n∈N),则此数列的通项为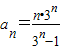 ,且{a n }不是比等差数列.
,且{a n }不是比等差数列. ▼优质解答
答案和解析
【答案】分析:根据比等差数列的定义(λ为常数),逐一判断①~④中的四个数列是否是比等差数列,即可得到答案.数列{Fn}满足F1=1,F2=1,F3=2,F4=3,F5=5,-=1,-=-≠1,则该数列不是比等差数列,故①正确;若数列{an}满足an=(n-1)•2n-1,则=不为定值,即数列{an}不是比等差数列,故②错误;等比数列=0,满足比等差数列的定义,若等差数列为an=n,则=不为定值,即数列{an}不是比等差数列,故③正确;数列{an}的通项公式为:,则,,,,=-,=-≠-,不满足比等差数列的定义,故④不正确;故答案为:①③点评:本题考查新定义,解题时应正确理解新定义,同时注意利用列举法判断命题为假,属于难题.
看了 在数列{an}中,如果对任意...的网友还看了以下:
用以下成语任选5个编一段文字80字以上.请注明所选词语.百身何赎 阪上走丸 半青半黄 暴殄天物 暴 2020-05-16 …
在三维空间直角坐标系中,对其中任何一向量x=(x1,x2,x3),定义范数||x||,它满足以下性 2020-05-17 …
现从8个校篮球队成员和2个校足球队成员组成的10人接力赛预备队中,任取2人,已知取出的有一个是足球 2020-05-17 …
高一数学,若定义在R上的函数f(x)满足:对任意x1,x2∈R,有f(x1+x2)=f(x1)+f 2020-05-22 …
在uC/OS-II中,OSSched()函数是任务调度的前导函数,用于判断进行任务调度的条件是否满足 2020-05-23 …
证明菱形时,满足的邻角互补,对角相等,是都满足?还是只满足他俩中的任意一个? 2020-06-18 …
高一数学题Sn={1,2,3...n}(n∈正整数)①A包含于Sn②任意x属于A→2x∉A③任意x 2020-07-30 …
已知非空集合A是由一些函数组成,满足如下性质:①对任意f(x)∈A,f(x)均存在反函数f-1(x 2020-08-01 …
请教一个正则表达式请问如何写一个正则表达式判断一些中文字符中是否满足以下任意一个条件中的一个,即可判 2020-11-01 …
已知无穷数列{an},a1=1,a2=2,对任意n∈N*,有an+2=an,数列{bn}满足bn+1 2020-11-06 …