如图，点A（-1，0）、B（1，0），点C在x轴正半轴上，过线段BC的n等分点Di作与BC垂直的射线li，在li上的动点P使∠APB取得最大值的位置记作Pi（i=1，2，3，…，n-1）．是否存在一条圆锥曲线，对

Question

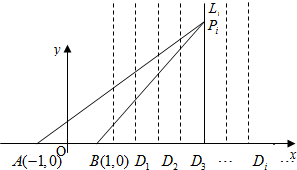
如图，点A（-1，0）、B（1，0），点C在x轴正半轴上，过线段BC的n等分点D_i作与BC垂直的射线l_i，在l_i上的动点P使∠APB取得最大值的位置记作P_i（i=1，2，3，…，n-1）．是否存在一条圆锥曲线，对任意的正整数n≥2，点P_i（i=1，2，…，n-1）都在这条曲线上？说明理由．

Answer 1

存在一条双曲线，对任意的正整数n≥2，点P_i（i=1，2，…，n-1）都在这条双曲线上．   
如图所示，A（-1，0），B（1，0），设|BC|=b，P（x，y），则x>1，y>0，x=(i)/(n)b，∠APB=∠PBC-∠PACtan∠PAC=(y)/(x+1)，tan∠PBC=(y)/(x-1)
所以tan∠APB=((y)/(x-1)-(y)/(x+1))/(1+(y2)/((x-1)(x+1)))=(2)/(((x-1)(x+1))/(y)+y)．    
当i=1，2，3，…，n-1一定时，x=(i)/(n)|BC|为常数
所以((x-1)(x+1))/(y)+y≥2√((x-1)(x+1))，此时tan∠APB取得最大值，
当且仅当((x-1)(x+1))/(y)=y时等号成立，
故x²-y²=1，x>1，y>0，P_i在一条双曲线上．