在学习勾股定理时，我们学会运用图（I）验证它的正确性；图中大正方形的面积可表示为：（a+b）2，也可表示为：c2+4•（12ab），即（a+b）2=c2+4•（12ab）由此推出勾股定理a2+b2=c2，这种根据

Question

在学习勾股定理时，我们学会运用图（I）验证它的正确性；图中大正方形的面积可表示为：
（a+b）²，也可表示为：c²+4•（(1)/(2)ab），
即（a+b）²=c²+4•（(1)/(2)ab）由此推出勾股定理a²+b²=c²，这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．

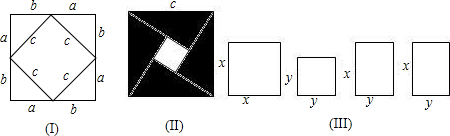
（1）请你用图（II）（2002年国际数字家大会会标）的面积表达式验证勾股定理（其中四个直角三角形全等）；
（2）请你用（III）提供的图形进行组合，用组合图形的面积表达式验证（x+y）²=x²+2xy+y²；
（3）请你自己设计图形的组合，用其面积表达式验证：（x+p）（x+q）=x²+px+qx+pq=x²+（p+q）x+pq．

Answer 1

（1）大正方形的面积为：c²，中间空白部分正方形面积为：（b-a）²；
四个阴影部分直角三角形面积和为：4×(1)/(2)ab；
由图形关系可知：大正方形面积=空白正方形面积+四直角三角形面积，即有：c²=（b-a）²+4×(1)/(2)ab=b²-2ab+a²+2ab=a²+b²；

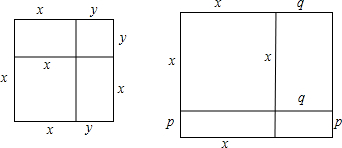
（2）如图示：大正方形边长为（x+y）所以面积为：（x+y）²，它的面积也等于两个边长分别为x，y和两个长为x宽为y的矩形面积之和，即x²+2xy+y²
所以有：（x+y）²=x²+2xy+y²成立；

（3）如图示：大矩形的长、宽分别为（x+p），（x+q），则其面积为：（x+p）•（x+q），从图形关系上可得大矩形为一个边长为x的正方形和三个小矩形构成的则其面积又可表示为：x²+px+qx+pq，则有：（x+p）（x+q）=x²+px+qx+pq=x²+（p+q）x+pq．