早教吧作业答案频道 -->数学-->
概念学习已知△ABC,点P为其内部一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形,其内角与△ABC的三个内角分别相等,那么就称点P为△ABC的等角点.理解应用(1)判断
题目详情
概念学习
已知△ABC,点P为其内部一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形,其内角与△ABC的三个内角分别相等,那么就称点P为△ABC的等角点.
理解应用
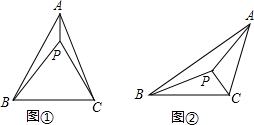
(1)判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真”;反之,则写“假”
①内角分别为30、60、90的三角形存在等角点;___
②任意的三角形都存在等角点.___
(2)探究图①中∠BPC、∠ABC、∠ACP之间的数量关系,并说明理由.
解决问题
如图②,在△ABC中,∠A<∠B<∠C,若△ABC的三个内角的角平分线的交点P是该三角形的等角点.求该三角形三个内角的度数.
已知△ABC,点P为其内部一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形,其内角与△ABC的三个内角分别相等,那么就称点P为△ABC的等角点.
理解应用

(1)判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真”;反之,则写“假”
①内角分别为30、60、90的三角形存在等角点;___
②任意的三角形都存在等角点.___
(2)探究图①中∠BPC、∠ABC、∠ACP之间的数量关系,并说明理由.
解决问题
如图②,在△ABC中,∠A<∠B<∠C,若△ABC的三个内角的角平分线的交点P是该三角形的等角点.求该三角形三个内角的度数.
▼优质解答
答案和解析
(1)①内角分别为30、60、90的三角形存在等角点是真命题;
②任意的三角形都存在等角点是假命题,如等边三角形不存在等角点;
故答案为:真,假;
(2)如图①,∵在△ABC中,∠BPC=∠ABP+∠BAC+∠ACP,∠BAC=∠PBC,
∴∠BPC=∠ABP+∠PBC+∠ACP=∠ABC+∠ACP;
(3)如图②,连接PB,PC
∵P为△ABC的角平分线的交点,
∴∠PBC=
∠ABC,∠PCB=
∠ACB,
∵P为△ABC的等角点,
∴∠PBC=∠A,∠BCP=∠ABC-2∠PBC=2∠A,∠ACB=∠BCP-4∠A,
又∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠A+4∠A=180°,
∴∠A=
,
∴该三角形三个内角的度数分别为
,
,
.
②任意的三角形都存在等角点是假命题,如等边三角形不存在等角点;
故答案为:真,假;
(2)如图①,∵在△ABC中,∠BPC=∠ABP+∠BAC+∠ACP,∠BAC=∠PBC,

∴∠BPC=∠ABP+∠PBC+∠ACP=∠ABC+∠ACP;
(3)如图②,连接PB,PC
∵P为△ABC的角平分线的交点,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵P为△ABC的等角点,
∴∠PBC=∠A,∠BCP=∠ABC-2∠PBC=2∠A,∠ACB=∠BCP-4∠A,
又∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠A+4∠A=180°,
∴∠A=
| 180° |
| 7 |
∴该三角形三个内角的度数分别为
| 180° |
| 7 |
| 360° |
| 7 |
| 720° |
| 7 |
看了概念学习已知△ABC,点P为其...的网友还看了以下:
一道质数证明题假设 p q r 分别为质数,其中p为奇数证明:如果(2p+r) 与 (2p-r) 2020-05-13 …
已知直线l:y=kx+1交曲线C:y=ax^2(a>0)于P、Q两点,M为PQ中点,分别过P、Q两 2020-05-15 …
一个容器中盛有水和煤油两种液体,在液体中悬浮着一块冰水、煤油、冰的密度分别为P水P油P冰,且P水> 2020-05-15 …
如图所示,当用扳手拧螺母时,扳手上的P、Q两点的角速度分别为ωP和ωQ,线速度大小分别为υP和υQ 2020-06-12 …
高数微积分设两种产品的需求量分别是x,y,相应的价格分别为p、q,已知x=1-p+2q,y=11+ 2020-06-14 …
甲、乙两人的质量分别为50kg和60kg,在登上同一座高楼的过程中,甲用了8分钟,乙用了10分钟, 2020-06-16 …
两个人的相遇与分别从P镇到Q镇有一条道路相同.A从P镇出发步行向Q镇走,A出发30分钟后B从Q镇出 2020-07-06 …
如图所示,取4个完全相同的正方体物块,分别以甲、乙、丙三种方式叠放(均放在中央位置),在三种叠放方 2020-07-07 …
(2014•西藏模拟)某静电场的电场线分布如图所示,图中P、Q两点的电场强度的大小分别为EP和EQ 2020-07-20 …
如图所示,甲、乙两个容器内装满质量相等的同种液体,容器底受到的压强分别为P甲、P乙,受到的压力分别为 2020-11-29 …