早教吧作业答案频道 -->数学-->
如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.(Ⅰ)求证:AB⊥PC;(Ⅱ)若三角形PAB是边长为2的等边三角形,求三棱锥P-ABC外接球的表面积.
题目详情
如图,四棱锥P-ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°.
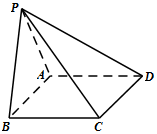
(Ⅰ)求证:AB⊥PC;
(Ⅱ)若三角形PAB是边长为2的等边三角形,求三棱锥P-ABC外接球的表面积.

(Ⅰ)求证:AB⊥PC;
(Ⅱ)若三角形PAB是边长为2的等边三角形,求三棱锥P-ABC外接球的表面积.
▼优质解答
答案和解析
证明:(Ⅰ)作PO⊥AB于O…①,连接OC,
∵平面PAB⊥平面ABCD,且面PAB∩面ABCD=AB,
∴PO⊥面ABCD.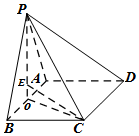
∵PB=PC,∴△POB≌△POC,∴OB=OC,
又∵∠ABC=45°,∴OC⊥AB…②
又PO∩CO=O,由①②,得AB⊥面POC,
又PC⊂面POC,∴AB⊥PC.…(6分)
(Ⅱ)∵三角形PAB是边长为2的等边三角形,
∴PO=
,OA=OB=OC=1.
∵PO⊥面ABCD,PO>OA=OB=OC,线段PO上取点E,
∴EA=EB=EC,E是外接球的球心,
设三棱锥P-ABC外接球的半径为R,
EO=
-R,EC=R,EC2=EO2+OC2,
R2=12+(
-R)2,R=
,
∴三棱锥P-ABC外接球的表面积S=4πR2=
.…(12分)
∵平面PAB⊥平面ABCD,且面PAB∩面ABCD=AB,
∴PO⊥面ABCD.

∵PB=PC,∴△POB≌△POC,∴OB=OC,
又∵∠ABC=45°,∴OC⊥AB…②
又PO∩CO=O,由①②,得AB⊥面POC,
又PC⊂面POC,∴AB⊥PC.…(6分)
(Ⅱ)∵三角形PAB是边长为2的等边三角形,
∴PO=
| 3 |
∵PO⊥面ABCD,PO>OA=OB=OC,线段PO上取点E,
∴EA=EB=EC,E是外接球的球心,
设三棱锥P-ABC外接球的半径为R,
EO=
| 3 |
R2=12+(
| 3 |
2
| ||
| 3 |
∴三棱锥P-ABC外接球的表面积S=4πR2=
| 16π |
| 3 |
看了如图,四棱锥P-ABCD的底面...的网友还看了以下:
平行四边形ABCD周长为20,O是对角线AC,BD的交点若△ABC的周长为17cm求OC的长若△A 2020-05-13 …
已知平行四边行ABCD的周长是80cm,BC=24cm,AE=5cm.一,求AB的长度.二,求A已 2020-05-16 …
如图,在平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,D 2020-06-02 …
如图所示,长方形ABCD的长为25,宽为15.四对平行线截长方形各边所得的线段的长已在图上标出,且 2020-06-13 …
如图所示,长方形ABCD的长为25,宽为15.四对平行线截长方形各边所得的线段的长已在图上标出,且 2020-06-13 …
如图所示,长方形ABCD的长为25,宽为15.四对平行线截长方形各边所得的线段的长已在图上标出,且 2020-06-14 …
在平行四边形ABCD中,AB=AC,若平行四边形周长为38CM三角形ABC的周长比平行四边形ABC 2020-07-24 …
已知平行四边行ABCD的对角线AC与BD,相交于O,这个平行四边形的周长是16.且三角形AOB的周长 2020-11-04 …
6.[2015•长沙]随着全民健身活动的蓬勃开展,每到周末,长沙市随处可见骑行自行车健身的市民。中学 2020-11-12 …
平行四边形的周长怎么求平行四边形的长是20厘米,高是12厘米,求周长不是长方形 2021-02-17 …