椭圆：（a＞b＞0），左右焦点分别是F1，F2，焦距为2c，若直线与椭圆交于M点，满足∠MF1F2=2∠MF2F1，则离心率是（）A．B．C．D．

Question

椭圆：（a＞b＞0），左右焦点分别是F₁，F₂，焦距为2c，若直线与椭圆交于M点，满足∠MF₁F₂=2∠MF₂F₁，则离心率是（　　）

A．  B．  C．  D．

Answer 1

B【考点】椭圆的简单性质．

【专题】计算题；圆锥曲线的定义、性质与方程．

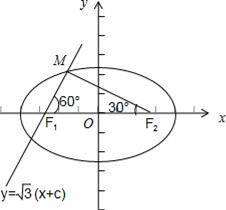
【分析】依题意知，直线y=（x+c）经过椭圆的左焦点F₁（﹣c，0），且倾斜角为60°，从而知∠MF₂F₁=30°，设|MF₁|=x，利用椭圆的定义即可求得其离心率．

【解答】∵椭圆的方程为+=1（a＞b＞0），作图如右图：

∵椭圆的焦距为2c，

∴直线y=（x+c）经过椭圆的左焦点F₁（﹣c，0），又直线y=（x+c）与椭圆交于M点，

∴倾斜角∠MF₁F₂=60°，又∠MF₁F₂=2∠MF₂F₁，

∴∠MF₂F₁=30°，

∴∠F₁MF₂=90°．

设|MF₁|=x，则|MF₂|=x，|F₁F₂|=2c=2x，故x=c．

∴|MF₁|+|MF₂|=（+1）x=（+1）c，

又|MF₁|+|MF₂|=2a，

∴2a=（+1）c，

∴该椭圆的离心率e===﹣1．

故选：B．

【点评】本题考查椭圆的简单性质，着重考查直线与椭圆的位置关系，突出椭圆定义的考查，理解得到直线y=（x+c）经过椭圆的左焦点F₁（﹣c，0）是关键，属于中档题．