直三棱柱ABC-A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E，要使AB1⊥平面C1DF，则线段B1F的长为（）A.12B.1C.32D.2

Question

直三棱柱ABC-A₁B₁C₁中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A₁B₁的中点，F是BB₁上的动点，AB₁，DF交于点E，要使AB₁⊥平面C₁DF，则线段B₁F的长为（　　）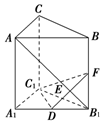

A.

(1)/(2)

B. 1

C.

(3)/(2)

D. 2

Answer 1

作DE⊥AB₁交AB₁于E，延长DE交BB₁于F，连接C₁F，则AB₁⊥平面C₁DF，点F即为所求．
∵C₁D⊥平面AA₁B₁B，AB₁⊂平面AA₁B₁B，
∴C₁D⊥AB₁．又AB₁⊥DF，DF∩C₁D=D，
∴AB₁⊥平面C₁DF．
四边形AA₁B₁B为正方形，此时点F为B₁B的中点．
如图则有△AA₁B₁∽DB₁F，即(AA1)/(DB1)=(A1B)/(B1F)⇒B1F=(1)/(2)．
故选：A