早教吧作业答案频道 -->数学-->
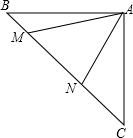
如图,等腰直角△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上,且∠MAN=45°,MB=1,CN=3,求MN的长.
题目详情
如图,等腰直角△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上,且∠MAN=45°,MB=1,CN=3,求MN的长.

▼优质解答
答案和解析
过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.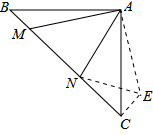
∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,
,
∴△ABM≌△ACE(SAS).
∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,
,
∴△MAN≌△EAN(SAS).
∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
∴MN2=BM2+NC2.
∵BM=1,CN=3,
∴MN2=12+32,
∴MN=
.

∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,
|
∴△ABM≌△ACE(SAS).
∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,
|
∴△MAN≌△EAN(SAS).
∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
∴MN2=BM2+NC2.
∵BM=1,CN=3,
∴MN2=12+32,
∴MN=
| 10 |
看了 如图,等腰直角△ABC中,∠...的网友还看了以下:
已知递增的等比数列{an}的前三项之积是64,且a2-1,a3-3,a4-9成等差数列.(1)求数 2020-05-13 …
已知递增的等比数列{an}的前三项之积是64,且a2-1,a3-3,a4-9成等差数列.(1)求数 2020-05-14 …
在等差数列{an}中,a4=-15,公差d=3,求数列{an}的前n项和Sn=3n-27(1)求∑ 2020-05-14 …
已知a,b,c为实数,且a2+b2+c2=9,求(a-b)2+(b-c)2+(c-a)2的最大值. 2020-05-15 …
设{a}为等差数列{b}为等比数列且a1=b1,若cn=an+bn且c1=2,c2=5,c3=9求 2020-05-15 …
已知实数等比数列{an}满足a1+a6=11,且a3a4=32/9.求数列{an}的通项公式;(2 2020-07-09 …
这个方程组怎么解?a+3q=a*q^3a+9q=a*q^9求a与qan是等差数列,bn是等比数列, 2020-07-09 …
菱形的两条对角线分别等于8和6,并且分别放置在X轴Y轴上,对角线的交点和原点重合.求各边所在的直线 2020-07-12 …
求a=b=c的值求AB:BM的值.(1)若a:b:c=3:5:7,且3a+2b-4c=9,且3a+2 2020-12-02 …
基本不等式求值域:当且仅当时,两项取向等,x无解(如x方=-8)不具备“相等”条件时,该怎么办?y= 2020-12-15 …