早教吧作业答案频道 -->数学-->
如图,反比例函数y=kx的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=kx在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-2时,求△OCD的面
题目详情
如图,反比例函数y=
的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=
在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.
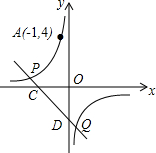
(1)求k的值;
(2)当b=-2时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.
| k |
| x |
| k |
| x |

(1)求k的值;
(2)当b=-2时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.
▼优质解答
答案和解析
(1)∵反比例函数y=
的图象经过点A(-1,4),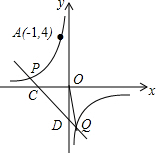
∴k=-1×4=-4;
(2)当b=-2时,直线解析式为y=-x-2,
∵y=0时,-x-2=0,解得x=-2,
∴C(-2,0),
∵当x=0时,y=-x-2=-2,
∴D(0,-2),
∴S△OCD=
×2×2=2;
(3)存在.
当y=0时,-x+b=0,解得x=b,则C(b,0),
∵S△ODQ=S△OCD,
∴点Q和点C到OD的距离相等,
而Q点在第四象限,
∴Q的横坐标为-b,
当x=-b时,y=-x+b=2b,则Q(-b,2b),
∵点Q在反比例函数y=-
的图象上,
∴-b•2b=-4,解得b=-
或b=
(舍去),
∴b的值为-
.
| k |
| x |

∴k=-1×4=-4;
(2)当b=-2时,直线解析式为y=-x-2,
∵y=0时,-x-2=0,解得x=-2,
∴C(-2,0),
∵当x=0时,y=-x-2=-2,
∴D(0,-2),
∴S△OCD=
| 1 |
| 2 |
(3)存在.
当y=0时,-x+b=0,解得x=b,则C(b,0),
∵S△ODQ=S△OCD,
∴点Q和点C到OD的距离相等,
而Q点在第四象限,
∴Q的横坐标为-b,
当x=-b时,y=-x+b=2b,则Q(-b,2b),
∵点Q在反比例函数y=-
| 4 |
| x |
∴-b•2b=-4,解得b=-
| 2 |
| 2 |
∴b的值为-
| 2 |
看了 如图,反比例函数y=kx的图...的网友还看了以下:
有一固定的带电量为Q的正点电荷,AB两点在Q点正上方和Q相距分别为h和0.25h,将另一带电小球从 2020-04-27 …
(1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的 2020-05-13 …
(1)等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的 2020-05-13 …
如图1,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动 2020-05-13 …
已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0)(0,3),现有两动点P, 2020-05-17 …
三道很难的数学题1:已知圆M:x^2+(y-2)^2=1,Q点是x轴上的一动点,QA,QB分别切圆 2020-06-13 …
如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动, 2020-06-18 …
如图,已知△ABC中∠A=60°,AB=2cm,AC=6cm,点P、Q分别是边AB、AC上的动点, 2020-06-19 …
(2014•海淀区模拟)已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、CC1、 2020-07-13 …
(2014•烟台模拟)如图所示,两个等量异种点电荷+Q、-Q分别固定在处于真空中的正方体的两个顶点上 2020-11-13 …