早教吧作业答案频道 -->数学-->
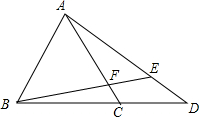
如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为.
题目详情
如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为___.

▼优质解答
答案和解析
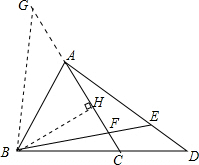 如图,延长CA至点G使GA=CD,连接GB,
如图,延长CA至点G使GA=CD,连接GB,
∵△ABC是等边三角形,
∴AB=CA,∠BAC=∠ACB=60°,
∴∠GAB=∠DCA=120°,
∴在△GBA与△DAC中,
,
∴△GBA≌△DAC(SAS),
∴BG=AD,
∵AF+CD=AD,AF+GA=GF,
∴GF=AD,
∴BG=GF.
∴∠GBF=∠GFB.
又∵∠GBA=∠CAD,
∴∠ABE=∠AEB,
∴AB=AE.
设AD=a,则BG=a,AB=AE=a-2,GA=GF-AF=BG-AF=a-4,
又∵∠GAB=120°,
∴作BH⊥AC,垂足为H,易求a=7,即AD=7.
故答案是:7.
 如图,延长CA至点G使GA=CD,连接GB,
如图,延长CA至点G使GA=CD,连接GB,∵△ABC是等边三角形,
∴AB=CA,∠BAC=∠ACB=60°,
∴∠GAB=∠DCA=120°,
∴在△GBA与△DAC中,
|
∴△GBA≌△DAC(SAS),
∴BG=AD,
∵AF+CD=AD,AF+GA=GF,
∴GF=AD,
∴BG=GF.
∴∠GBF=∠GFB.
又∵∠GBA=∠CAD,
∴∠ABE=∠AEB,
∴AB=AE.
设AD=a,则BG=a,AB=AE=a-2,GA=GF-AF=BG-AF=a-4,
又∵∠GAB=120°,
∴作BH⊥AC,垂足为H,易求a=7,即AD=7.
故答案是:7.
看了 如图,△ABC是等边三角形,...的网友还看了以下:
如题A比B大四分之一,A是B的什么,B比A小多少?里面都应该填分数第二个问题好像是五分之一,第一个不 2020-03-30 …
下面错误的说法是()A.一个数(零除外)与它的倒数的乘积等于1B.已知a×1314=b(a是非零自 2020-04-07 …
a和b都是整数,且a÷b=2…1,下列说法正确的是()A.a是偶数B.a是奇数C.b是偶数D.b是 2020-04-09 …
有A、B两种烃,含碳元素的质量分数相等,下列关于A和B的叙述正确的是( )A. A和B一定是同分 2020-05-13 …
若A和B都是五次多项式,则A+B一定是( )A. 十次多项式B. 五次多项式C. 数次不高于5的 2020-05-14 …
若A是三次多项式 B是二次多项式 则A-B一定是()A.五次整式B.三次整式C.二次整式D.一次整 2020-05-16 …
若A是一个三次多项式,B是一个四次多项式,则A+B一定是().A.三次多项式 B.四次多项式 C. 2020-05-16 …
有A.B两种烃,含碳的质量分数相同,关于A和B的叙述中正确的是A,A和B的最简式相同B.A和B一定 2020-05-16 …
A、B两种烃,它们含碳质量分数相同,下列关于A和B的叙述正确的是 ()A.A和B一定是同分异构体 2020-05-16 …
有A、B两种烃,含碳的质量分数相同,关于A和B关系的下列叙述中正确有A、B两种烃,含碳的质量分数相 2020-05-16 …