问题情境：如图1，已知△ABC和△DCE中，∠ACB=∠DCE=90°，AC=BC=2，CD=CE=1，点D在AC边上，点E在BC延长线上，将△DCE从此位置开始绕C点顺时针旋转，旋转角是α（0

Question

问题情境：
如图1，已知△ABC和△DCE中，∠ACB=∠DCE=90°，AC=BC= √(2)，CD=CE=1，点D在AC边上，点E在BC延长线上，将△DCE从此位置开始绕C点顺时针旋转，旋转角是α（0°<α<180°）
操作发现：

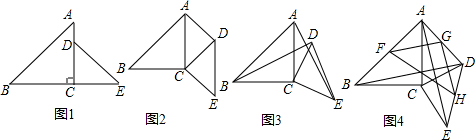
（1）如图2，当旋转角α=45°时，连接AD．求证：四边形ACED是平行四边形；
 （2）如图3，当°<α<90°时，连接BD，AE，判断线段BD与AE的数量关系，并说明理由；
解决问题：
（3）如图3，当0°<α<180°时，连接AD，点F，G，H分别是线段AB，AD，DE的中点，连接FG，GH，FH，在△CDE旋转的过程中，AE与BD的数量关系是___．所以△FGH始终是一个特殊三角形，当旋转角α=135°时，△FGH的面积是___．问题情境：
如图1，已知△ABC和△DCE中，∠ACB=∠DCE=90°，AC=BC= √(2)，CD=CE=1，点D在AC边上，点E在BC延长线上，将△DCE从此位置开始绕C点顺时针旋转，旋转角是α（0°<α<180°）
操作发现：

（1）如图2，当旋转角α=45°时，连接AD．求证：四边形ACED是平行四边形；
 （2）如图3，当°<α<90°时，连接BD，AE，判断线段BD与AE的数量关系，并说明理由；
解决问题：
（3）如图3，当0°<α<180°时，连接AD，点F，G，H分别是线段AB，AD，DE的中点，连接FG，GH，FH，在△CDE旋转的过程中，AE与BD的数量关系是___．所以△FGH始终是一个特殊三角形，当旋转角α=135°时，△FGH的面积是___．
√(2)，CD=CE=1，点D在AC边上，点E在BC延长线上，将△DCE从此位置开始绕C点顺时针旋转，旋转角是α（0°<α<180°）
操作发现：

（1）如图2，当旋转角α=45°时，连接AD．求证：四边形ACED是平行四边形；
 （2）如图3，当°<α<90°时，连接BD，AE，判断线段BD与AE的数量关系，并说明理由；
解决问题：
（3）如图3，当0°<α<180°时，连接AD，点F，G，H分别是线段AB，AD，DE的中点，连接FG，GH，FH，在△CDE旋转的过程中，AE与BD的数量关系是___．所以△FGH始终是一个特殊三角形，当旋转角α=135°时，△FGH的面积是___．√(2)

2

2

2

Answer 1

（1）证明：在RT△DCE中，∵DC=CE=1，∴DE=2，∴AC=DE，∵∠ACD=∠ECD=45°，∴DE∥AC，∴四边形ACDE是平行四边形．（2）BD=AE．如图，理由：∵∠ABC=∠DCE=90°，∴∠ABC+α=∠DCE+α，∴∠BCD=∠ACE，在△BCD和△A...