早教吧作业答案频道 -->数学-->
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.(Ⅰ)求证:AB1⊥面PBC;(Ⅱ)在BC边上找一点Q,使PQ∥面A1ABB1,并求三棱锥Q-PBB1的体积.
题目详情
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.
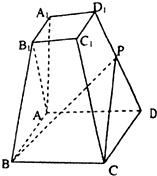
(Ⅰ)求证:AB1⊥面PBC;
(Ⅱ)在BC边上找一点Q,使PQ∥面A1ABB1,并求三棱锥Q-PBB1的体积.

(Ⅰ)求证:AB1⊥面PBC;
(Ⅱ)在BC边上找一点Q,使PQ∥面A1ABB1,并求三棱锥Q-PBB1的体积.
▼优质解答
答案和解析
解(1)取AA1中点M,连结BM,PM,
在PM∥AD∥BC,∴BM⊂平面PBC.
∵AA1⊥面ABCD,BC⊂面ABCD,∴AA1⊥BC,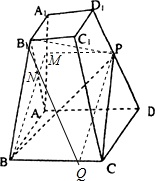
∵ABCD是正方形,∴AB⊥BC,
又AB⊂平面ABB1A1,AA1⊂平面ABB1A1,AB∩AA1=A,
∴BC⊥平面ABB1A1,∵AB1⊂平面ABB1A1,
∴BC⊥AB1.
∵AB=AA1=4,∠BAM=∠B1A1A=90°,AM=B1A1=2,
∴△ABM≌△A1AB1,∴∠MBA=∠B1AA1,
∵∠BAB1+∠B1AA1=90°,∴∠MBA+∠BAB1=90°,
∴BM⊥AB1,
∵BM⊂平面PBC,BC⊂平面PBC,BM∩BC=B,
∴AB1⊥面PBC.
(2)在BC边上取一点Q,使BQ=3,
∵PM为梯形ADD1A1的中位线,A1D1=2,AD=4,
∴PM=3,PM∥AD,又∵BQ∥AD,
∴PM
BQ,
∴四边形PMBQ是平行四边形,
∴PQ∥BM,又BM⊂平面A1ABB1,PQ⊄平面A1ABB1,
∴PQ∥平面A1ABB1.
∵BC⊥平面ABB1A1,BM⊂平面ABB1A1,
∴BQ⊥BM,
∵AB=AA1=4,AM=A1B1=2,∴BM=AB1=2
,
设AB1∩BM=N,则AN=
=
.∴B1N=AB1-AN=
.
∴V B1-BPQ=
S△BPQ•B1N=
×
×3×2
×
=6.
在PM∥AD∥BC,∴BM⊂平面PBC.
∵AA1⊥面ABCD,BC⊂面ABCD,∴AA1⊥BC,

∵ABCD是正方形,∴AB⊥BC,
又AB⊂平面ABB1A1,AA1⊂平面ABB1A1,AB∩AA1=A,
∴BC⊥平面ABB1A1,∵AB1⊂平面ABB1A1,
∴BC⊥AB1.
∵AB=AA1=4,∠BAM=∠B1A1A=90°,AM=B1A1=2,
∴△ABM≌△A1AB1,∴∠MBA=∠B1AA1,
∵∠BAB1+∠B1AA1=90°,∴∠MBA+∠BAB1=90°,
∴BM⊥AB1,
∵BM⊂平面PBC,BC⊂平面PBC,BM∩BC=B,
∴AB1⊥面PBC.
(2)在BC边上取一点Q,使BQ=3,
∵PM为梯形ADD1A1的中位线,A1D1=2,AD=4,
∴PM=3,PM∥AD,又∵BQ∥AD,
∴PM
| ∥ |
. |
∴四边形PMBQ是平行四边形,
∴PQ∥BM,又BM⊂平面A1ABB1,PQ⊄平面A1ABB1,
∴PQ∥平面A1ABB1.
∵BC⊥平面ABB1A1,BM⊂平面ABB1A1,
∴BQ⊥BM,
∵AB=AA1=4,AM=A1B1=2,∴BM=AB1=2
| 5 |
设AB1∩BM=N,则AN=
| AB•AM |
| BM |
4
| ||
| 5 |
6
| ||
| 5 |
∴V B1-BPQ=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
6
| ||
| 5 |
看了 已知四棱台ABCD-A1B1...的网友还看了以下:
P(A/B)+P(A非/B非)=1证明AB独立我这样证:原始=P(A/B)+1-P(A/B非)=1 2020-04-06 …
概率基本公式歧义性,我用'符号表示非A,B为两个事件,求恰好有一个发生的概率.P(AB'∪A'B) 2020-05-13 …
设有A,B,C,三个事件,已知A与C互不相容,B与C相互独立,且P(A)=1/12,P(B)=1/ 2020-05-13 …
概率加法公式加法公式,对于任意两事件A,B,有P(A并B)=P(A)+P(B)-P(AB)成立,假 2020-05-16 …
在概率论中:P(A-B)的数学意义是什么?看到有人这样解释:当B属于A时,P(A-B)=P(A)- 2020-05-16 …
已知P(A)=0.3,P(B)=0.5,P(AB)=0.15,验证P(B┃A)=P(B),P(B┃ 2020-06-12 …
1,P(A)=0.4P(AB)=0.2P(A|B)+P(A非|B非)=1求P(A并B)2,证明若P 2020-06-14 …
已知P(A)=0.3,P(B)=0.5,P(AB)=0.15,验证:P(B|A)=P(B),P(B 2020-06-22 …
集合A的幂集P(A)是集合A所有子集的集合求证P(A)∩P(B)=P(A∩B)麻烦写下具体步骤 2020-07-25 …
P(B/A)表示什么意思?是代表在A事件发生的条件下,B事件发生的概率?可是又怎么理解这句话呢?怎 2020-07-30 …