早教吧作业答案频道 -->数学-->
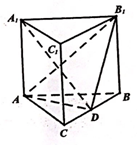
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为π3,点D线段BC的中点.(1)若AB=AC,求证:平面BB1C1C⊥平面AB1D;(2)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所
题目详情
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为
,点D线段BC的中点.
(1)若AB=AC,求证:平面BB1C1C⊥平面AB1D;
(2)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所成角θ的正弦值.
| π |
| 3 |

(1)若AB=AC,求证:平面BB1C1C⊥平面AB1D;
(2)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所成角θ的正弦值.
▼优质解答
答案和解析
(1)证明:由题意,∠ACB=
,AB=AC,
∴△ABC为正三角形,∴AD⊥BC,AD⊥CC1,
∴AD⊥平面BB1C1C,
∵AD⊂平面AB1D,
∴平面BB1C1C⊥平面AB1D;
(2) 当三棱柱ABC-A1B1C1的底面积最大时,体积最大,
∵4=AB2=AC2+BC2-2AC•BC•
≥AC•BC-AC•BC=AC•BC,
∴当AC=BC,三角形ABC为正三角形时面积取最大值,
设A1到平面AB1D的距离为d,则由等体积可得
S△AB1D•d=
•
•AD•DB1•d=
,
∴d=
,
∴sinθ=
=
=
.
| π |
| 3 |
∴△ABC为正三角形,∴AD⊥BC,AD⊥CC1,
∴AD⊥平面BB1C1C,
∵AD⊂平面AB1D,
∴平面BB1C1C⊥平面AB1D;
(2) 当三棱柱ABC-A1B1C1的底面积最大时,体积最大,
∵4=AB2=AC2+BC2-2AC•BC•
| 1 |
| 2 |
∴当AC=BC,三角形ABC为正三角形时面积取最大值,
设A1到平面AB1D的距离为d,则由等体积可得
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
∴d=
| 2 | ||
|
∴sinθ=
| d |
| A1D |
| ||||
|
2
| ||
| 35 |
看了 如图,已知在直三棱柱ABC-...的网友还看了以下:
求一数列.高2.a(n+1)=2an/2an+1已知a1=1a(n+1)=2an/2an+1求数列 2020-04-25 …
数学题: 已知抛物线y=x²+bx+c交x轴于A(1,0),B(3,0), 交y轴于点C,其顶点为 2020-05-13 …
1.设向量a、b满足/a/=2√5,b=(2,1),且a的模与b的模方向相反,求a的模.2.在▲A 2020-05-14 …
已知S=1+(-1/2)+1/2+(-1/3+1/3+(-1/4)+.+1/2014+(-1/20 2020-06-11 …
1.已知点A(0,1),B(1,0),c(1,2)D(2,1),试判断向量A到B和C到D的位置关系 2020-06-21 …
在等差数列{an}中,(1)已知a3=31,a7=76,求a1和d(2)已知a4=4,a8=-4, 2020-07-09 …
区间(c,d),[c,d],(c,d],[c,d)的长度均为d-c,已知a大于b,则求1/(x-a 2020-07-25 …
已知:∠1=∠2,∠C=∠D,求证:∠A=∠F证明:∵∠2=∠3()∠2=∠1(已知)∴∠1=∠3 2020-08-02 …
如图,已知∠1+∠2=180°,∠1=∠D,求证:BC∥DE.证明:∵∠1+∠2=108°(已知) 2020-08-02 …
1.已知m+n=5,1-p=-2,求-1+m+p+n的值.2.如果abcd是四个不相等的整数,且a* 2020-12-08 …