早教吧作业答案频道 -->数学-->
在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.(1)求∠EFD的度数;(2)判断FE与FD之间的数量关系,并证明你的结论.
题目详情
在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
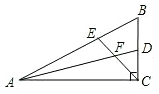
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.

(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
▼优质解答
答案和解析
(1)∵△ABC中,∠ACB=90°,∠B=60°
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=
∠BAC=15°,∠FCA=
∠ACB=45°
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
(2)FE与FD之间的数量关系为FE=FD;
证明:在AC上截取AG=AE,连接FG,
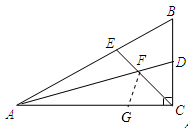
∵AD是∠BAC的平分线,∴∠1=∠2
又∵AF为公共边
在△EAF和△GAF中
∵
,
∴△AEF≌△AGF
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°,
又∵FC为公共边,∠DCF=∠FCG=45°
在△FDC和△FGC中
∵
,
∴△CFG≌△CFD,
∴FG=FD
∴FE=FD.
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
(2)FE与FD之间的数量关系为FE=FD;
证明:在AC上截取AG=AE,连接FG,

∵AD是∠BAC的平分线,∴∠1=∠2
又∵AF为公共边
在△EAF和△GAF中
∵
|
∴△AEF≌△AGF
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°,
又∵FC为公共边,∠DCF=∠FCG=45°
在△FDC和△FGC中
∵
|
∴△CFG≌△CFD,
∴FG=FD
∴FE=FD.
看了 在直角△ABC中,∠ACB=...的网友还看了以下:
△ABC中,AD垂直BC,E平分AC,BC=14,AD=12,sinB=0.8,求CD长和tan角 2020-06-03 …
如图,平行四边形ABCD的顶点A的坐标为(-32,0),顶点D在双曲线y=kx(x>0)上,AD交 2020-06-14 …
在三角形中,AD为Bc上中线,E为Ac上任一点,BE交AD午点0,当AE与Ac的比值...在三角形 2020-06-15 …
(2002•泰州)等腰梯形ABCD中,AD∥BC,AB=CD,面积S=9,建立如图所示的直角坐标系 2020-07-21 …
如图,平行四边形ABCD的顶点A的坐标为(-2,0),顶点D在双曲线y=kx(x>0)上,AD交y 2020-07-22 …
如图,矩形ABCD的边AD在y轴上,AD的中点与原点O重合,AB=1,AD=2,过定点P(3,0) 2020-07-30 …
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E 2020-07-31 …
如图,在平面直角坐标系,△ABC的顶点A(-3,0),B(0.3),AD⊥BC于D交Y轴于点E(0, 2020-11-01 …
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2A 2020-11-02 …
如图所示.在矩形ABCD中.已知AB等于二分之一AD.E是AD的中点.沿BE将三角形ABE折起至三角 2020-11-03 …