早教吧作业答案频道 -->数学-->
对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:①f(x1+x2)=f(x1)f(x2);②f=f(x1)+f(x2);③(x1-x2)[f(x1)-f(x2)]<0;④.当f(x)=2-x
题目详情
对于函数f(x)定义域中任意的x 1 ,x 2 (x 1 ≠x 2 ),有如下结论:
①f(x 1 +x 2 )=f(x 1 )f(x 2 );②f=f(x 1 )+f(x 2 );
③(x 1 -x 2 )[f(x 1 )-f(x 2 )]<0;④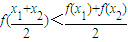 .
.
当f(x)=2 -x 时,上述结论中正确结论的序号是 写出全部正确结论的序号)
①f(x 1 +x 2 )=f(x 1 )f(x 2 );②f=f(x 1 )+f(x 2 );
③(x 1 -x 2 )[f(x 1 )-f(x 2 )]<0;④
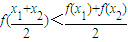 .
.当f(x)=2 -x 时,上述结论中正确结论的序号是 写出全部正确结论的序号)
▼优质解答
答案和解析
分析:
利用幂的运算法则判断出①对;通过举反例判断出②错;通过函数单调性的定义判断出③对;通过基本不等式判断出④对.
例如f(x)=2-x∴对于①,f(x1+x2)=,f(x1)f(x2)=,故①对对于②,f(x1•x2)=≠=f(x1)+f(x2);故②错对于③,∵为减函数,所以当x1>x2时,有f(x1)<f(x2),有(x1-x2)[f(x1)-f(x2)]<0对.对于④,,,有基本不等式,所以故④对故答案为①③④
点评:
判断多个命题的正误时,需要对各个命题依次判断.利用基本不等式求最值时,需要注意:一正、二定、三相等.
分析:
利用幂的运算法则判断出①对;通过举反例判断出②错;通过函数单调性的定义判断出③对;通过基本不等式判断出④对.
例如f(x)=2-x∴对于①,f(x1+x2)=,f(x1)f(x2)=,故①对对于②,f(x1•x2)=≠=f(x1)+f(x2);故②错对于③,∵为减函数,所以当x1>x2时,有f(x1)<f(x2),有(x1-x2)[f(x1)-f(x2)]<0对.对于④,,,有基本不等式,所以故④对故答案为①③④
点评:
判断多个命题的正误时,需要对各个命题依次判断.利用基本不等式求最值时,需要注意:一正、二定、三相等.
看了 对于函数f(x)定义域中任意...的网友还看了以下:
已知f(x)是定义在(0,+∞)上的函数,对任意两个不相等的正数x1,x2,都有x2f(x1)−x 2020-05-17 …
已知f(x)=根号(1+x^2)定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2( 2020-05-22 …
已知定义在D=[-4,4]上的函数f(x)=|x2+5x+4|,−4≤x≤02|x−2|,0<x≤ 2020-07-09 …
命题“若x2<1,则-1<x<1”的逆否命题是[]A.若x2≥1,则x≥1或x≤-1B.若-1<x 2020-08-01 …
已知f(x)=e^x,g(x)=lnx(1)求证g(x)<x<f(x)(2)设直线L与f(x),g( 2020-10-31 …
已知函数f(x)=a(x2+1)+x−1x−lnx(a∈R).(1)当a<12时,讨论f(x)的单调 2020-11-02 …
下列函数中,可以作为某个随机变量的分布函数是()A.F1(x)=1+x2,-∞<x<+∞B.F2(x 2020-11-03 …
(2013•肇庆二模)已知集合M={x|0<x<3},N={x|x2-5x+4≥0},则M∩N=() 2020-11-12 …
(2014•鄂州模拟)当0<x<1时,f(x)=sinxx,则下列大小关系正确的是()A.f2(x) 2020-11-12 …
概率问题、.p(x1<X≤x2)=.分布函数F(x)=.(a≤x<b)为什么范围要这么写.还有连续的 2020-12-26 …