早教吧作业答案频道 -->数学-->
如图,正方形ABCF和正方形CEFG,将正方形CEFG绕C顺时针旋转(1)如图1,求证:BE=DG;(2)当旋转到如图2位置时,此时A,F,C共线,点H为AF中点,连接BH,GH,试探究BH与GH的关系;(3)如图3
题目详情
如图,正方形ABCF和正方形CEFG,将正方形CEFG绕C顺时针旋转
(1)如图1,求证:BE=DG;
(2)当旋转到如图2位置时,此时A,F,C共线,点H为AF中点,连接BH,GH,试探究BH与GH的关系;
(3)如图3,若AB=5,CG=2,在旋转过程中,连接BG,DE,请直接写出BG2+DE2的值.
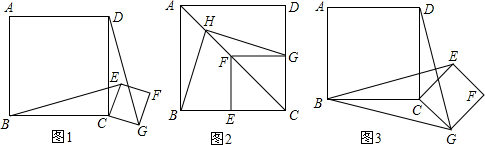
(1)如图1,求证:BE=DG;
(2)当旋转到如图2位置时,此时A,F,C共线,点H为AF中点,连接BH,GH,试探究BH与GH的关系;
(3)如图3,若AB=5,CG=2,在旋转过程中,连接BG,DE,请直接写出BG2+DE2的值.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD和EFGC都为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCE+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,
在△BCE和△DCG中,
,
∴△BCE≌△DCG(SAS),
∴BE=DG;
(2)BH=HG,理由为:
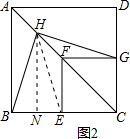
取BE的中点N,连接HN,HE,如图2所示,
∵AB∥CG∥FE,H是AF的中点,N为BE的中点,
∴HN是梯形ABEF的中位线,
∴HN∥AB,
∴HN⊥BE,
∵BN=NE,
∴BH=HE,
∵CE=CG,∠ECG=∠ECG=45°,CH=CH,
∴△HEC≌△HGC(SAS),
∴BH=HG;
(3)由(1)得:△BCE≌△DCG,
∴∠1=∠2,
∵∠1+∠4=∠3+∠1=90°,
∴∠2+∠3=90°,
∴∠BOC=90°,
连接BD,EG,如图3所示,
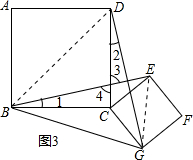
∴DO2+BO2=BD2=BC2+CD2=50,EO2+OG2=EG2=CG2+CE2=8,
则BG2+DE2=DO2+BO2+EO2+OG2=58.
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCE+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,
在△BCE和△DCG中,
|
∴△BCE≌△DCG(SAS),
∴BE=DG;
(2)BH=HG,理由为:

取BE的中点N,连接HN,HE,如图2所示,
∵AB∥CG∥FE,H是AF的中点,N为BE的中点,
∴HN是梯形ABEF的中位线,
∴HN∥AB,
∴HN⊥BE,
∵BN=NE,
∴BH=HE,
∵CE=CG,∠ECG=∠ECG=45°,CH=CH,
∴△HEC≌△HGC(SAS),
∴BH=HG;
(3)由(1)得:△BCE≌△DCG,
∴∠1=∠2,
∵∠1+∠4=∠3+∠1=90°,
∴∠2+∠3=90°,
∴∠BOC=90°,
连接BD,EG,如图3所示,

∴DO2+BO2=BD2=BC2+CD2=50,EO2+OG2=EG2=CG2+CE2=8,
则BG2+DE2=DO2+BO2+EO2+OG2=58.
看了 如图,正方形ABCF和正方形...的网友还看了以下:
一道简单的二阶导数和一道简单的不定积分1,设f"(x)存在,证明lim(h->0)[f(x0+h) 2020-05-13 …
图中ABCDEFGH分别代表oneeight8个英语数字,你能说出它们各代表几吗?A-B=C|*D 2020-05-13 …
已知f(x)在[0,1]连续,(0,1)可导,且f(0)=0,f(1)=1/2,试证明存在不同的h 2020-05-14 …
变限积分求道问题对函数f(t+h)-f(t-h)在[-h,h]上的积分对h求导.F(h)=∫[-h 2020-05-23 …
f(0)=0,则f(x)在x=0处可导的充要条件为A.lim(1/h^2)f(1-cosh),h→ 2020-06-12 …
f(0)=0,则f(x)在x=0处可导的充要条件为A.lim(1/h^2)f(1-cosh),h→ 2020-06-18 …
导数乘法证明中h是什么意思?(f(x)g(x))'=lim(h→0)[f(x+h)g(x+h)-f 2020-07-22 …
一道高数题目设f(x)在x=a的某个临域内有定义,则f(x)在x=a处可导的一个充分条件是()(A 2020-07-30 …
求导不同思路引起的不同结果习题:设f(x)的二阶导数存在,求lim[f(x+2h)-2f(x+h)+ 2020-11-03 …
导数运算求函数f(x)在x0处可求导,试求下列个极限的值LIMH→0f(x0+h)-f(x0-h)/ 2020-11-20 …