在半径为1的半圆中，作如图所示的等腰梯形ABCD，CE垂直下底AD于E，设DE=x（0＜x＜1），CE=h，梯形ABCD的周长为L．（1）求h关于x的函数解析式，并指出定义域；（2）试写出L与关于x的函

Question

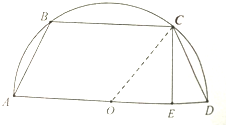在半径为1的半圆中，作如图所示的等腰梯形ABCD，CE垂直下底AD于E，设DE=x（0＜x＜1），CE=h，梯形ABCD的周长为L．
（1）求h关于x的函数解析式，并指出定义域；
（2）试写出L与关于x的函数解析式，并求周长L的最大值．

Answer 1

考点：
函数解析式的求解及常用方法
专题：
函数的性质及应用
分析：
（1）根据图形，便有h=1-(1-x)2=-x2+2x，并且定义域为（0，1）；（2）容易求出|CD|=2x，|BC|=2-2x，所以周长L=-2x+22x+4，对该函数解析式配方即可求出周长L的最大值．

（1）h2=1-（1-x）2=-x2+2x；∴h=-x2+2x，定义域为（0，1）；（2）如图，|CD|=h2+x2=2x；|BC|=2-2x；∴L=22x+2-2x+2=22x-2x+4=-2(x-22)2+5，x∈（0，1）；即L=-2(x-22)2+5，x∈（0，1）；∴x=22，即x=12时，L取最大值5．
点评：
考查根据实际问题求函数解析式的方法，直角三角形边的关系，梯形周长的概念，以及配方求函数最大值的方法．