早教吧作业答案频道 -->数学-->
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,连接OH.(1)求AD与DH的长;(2)求证:∠HDO=∠DCO.
题目详情
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,连接OH.
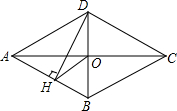
(1)求AD与DH的长;
(2)求证:∠HDO=∠DCO.

(1)求AD与DH的长;
(2)求证:∠HDO=∠DCO.
▼优质解答
答案和解析
 (1) ∵四边形ABCD是菱形,
(1) ∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=
AC=4cm,OB=OD=3cm,
∴AB=AD=5cm,
∴S菱形ABCD=
AC•BD=AB•DH,
∴DH=
=4.8(cm);
(2)证明:∵AB∥CD,
∴∠ABD=∠CDB,
∵∠ABD+∠HDO=90°,∠CDB+∠DCO=90°,
∴∠HDO=∠DCO.
 (1) ∵四边形ABCD是菱形,
(1) ∵四边形ABCD是菱形,∴AC⊥BD,OA=OC=
| 1 |
| 2 |
∴AB=AD=5cm,
∴S菱形ABCD=
| 1 |
| 2 |
∴DH=
| AC•BD |
| 2AB |
(2)证明:∵AB∥CD,
∴∠ABD=∠CDB,
∵∠ABD+∠HDO=90°,∠CDB+∠DCO=90°,
∴∠HDO=∠DCO.
看了 如图,四边形ABCD是菱形,...的网友还看了以下:
几道高二不等式题1.已知实数abc满足a>b>c,且a+b+c=1,a^2+b^2+c^2=1求证: 2020-03-30 …
已知a+b+c=1,求证:(a/1+b+c)+(b/1+a+c)+(c/1+a+b)≥3/5已知a 2020-04-05 …
证明不等式是什么时候要论证等号的成立比如说“若a,b,c为正实数,且a*b+b*c+c*a=0,用 2020-06-03 …
解几个与不等式有关的问题设a,b,c,d均为不等于0的实数,求证:∣b/a∣+∣b/c∣∣c/d∣ 2020-06-06 …
[20分][高一不等式]已知a,b,c∈R+,且a+b+c=1,求证1/a+1/b+1/c≥9已知 2020-06-10 …
a.b.c是三个不全相等的正数,且a+b+c=1,求证1-a/a+1-b/b+1-c/c>6求证( 2020-06-12 …
高二数学题,帮忙解决,要步骤的(1)设a,b,c属于R,a+b+c=0,abc0.(2)设a,b, 2020-07-22 …
一条关于推理与证明的问题用综合法证明:已知a,b,c已知a.b.c∈R,且a+b+c=1,求证:( 2020-08-01 …
已知a>0b>0a+b=1求证[1/a平方-1][1/b平方-1]已知a>0b>0a+b=1求证[1 2020-11-01 …
请问f(x)=a^x-b^x(a>b>1)是单增的吗?怎么证?1>a>b时呢?请问f(x)=a^x- 2020-11-03 …