早教吧作业答案频道 -->数学-->
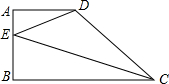
在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=3,BC=6,如果CE平分∠BCD交边AB于点E,那么DE的长为.
题目详情
在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=3,BC=6,如果CE平分∠BCD交边AB于点E,那么DE的长为___.



▼优质解答
答案和解析
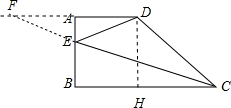 作DH⊥BC于点H,延长CE交DA的延长线于点F,
作DH⊥BC于点H,延长CE交DA的延长线于点F,
∵AD=2,AB=3,BC=6,
∴CH=6-2=4,DH=3,
∴CD=5,
∵CE平分∠BCD交边AB于点E,AD∥BC,AB⊥BC,
∴∠DCF=∠BDF=∠DFC,
∴DF=DC=5,
∴AF=3,
∴△FAE∽△CBE,
∴
=
,
即
=
,
∵AE+BE=3,
解得,AE=1,
∴DE=
=
=
,
故答案为:
.
AF BC AF AF AFBC BC BC=
AE BE AE AE AEBE BE BE,
即
=
,
∵AE+BE=3,
解得,AE=1,
∴DE=
=
=
,
故答案为:
.
3 6 3 3 36 6 6=
AE BE AE AE AEBE BE BE,
∵AE+BE=3,
解得,AE=1,
∴DE=
=
=
,
故答案为:
.
AE2+AD2 AE2+AD2 AE2+AD2 AE2+AD22+AD22=
12+22 12+22 12+22 12+222+222=
5 5 5 5,
故答案为:
.
5 5 5 5.
 作DH⊥BC于点H,延长CE交DA的延长线于点F,
作DH⊥BC于点H,延长CE交DA的延长线于点F,∵AD=2,AB=3,BC=6,
∴CH=6-2=4,DH=3,
∴CD=5,
∵CE平分∠BCD交边AB于点E,AD∥BC,AB⊥BC,
∴∠DCF=∠BDF=∠DFC,
∴DF=DC=5,
∴AF=3,
∴△FAE∽△CBE,
∴
| AF |
| BC |
| AE |
| BE |
即
| 3 |
| 6 |
| AE |
| BE |
∵AE+BE=3,
解得,AE=1,
∴DE=
| AE2+AD2 |
| 12+22 |
| 5 |
故答案为:
| 5 |
| AF |
| BC |
| AE |
| BE |
即
| 3 |
| 6 |
| AE |
| BE |
∵AE+BE=3,
解得,AE=1,
∴DE=
| AE2+AD2 |
| 12+22 |
| 5 |
故答案为:
| 5 |
| 3 |
| 6 |
| AE |
| BE |
∵AE+BE=3,
解得,AE=1,
∴DE=
| AE2+AD2 |
| 12+22 |
| 5 |
故答案为:
| 5 |
| AE2+AD2 |
| 12+22 |
| 5 |
故答案为:
| 5 |
| 5 |
看了 在梯形ABCD中,AD∥BC...的网友还看了以下:
设a,b,c分别是三角形ABC的三个内角A,B,C所对的边,则a^2=b(b+c)是A=2B的什么 2020-04-05 …
设a,b,c分别是三角形ABC的三个内角A,B,C所对的边,则a^2=b(b+c)是A=2B的什么 2020-04-05 …
设a,b,c分别是三角形ABC的三个内角,A,B,C所对的边.则a的平方=b(b+c)是A=2B的 2020-04-05 …
已知a.b.c分别是三角形ABC的三个内角A.B.C所对的边,若三角形ABC面积S三角形ABC=2 2020-04-05 …
若b+c分之a=c+a分之b=a+b分之c,则a+b-3c分之2a+2b+c=或(2)若关于x的方 2020-04-06 …
设a,b,c分别是三角形ABC的三个内角,A,B,C所对的边.则a的平方=b(b+c)是A=2B的 2020-05-15 …
在△ABC中a,b,c分别是叫A,B,C的对边,已知角A为锐角,且(sinA)^2-(cosA)^ 2020-05-16 …
在三角形ABC中,角A、B、C的对边长分别为a、b、c,若cos(90度+A)的平房+cosA=4 2020-05-20 …
1、已知:a+b+c=0,求:a(b分之1+c分之1)+b(c分之1+a分之1)+c(a分之1+b 2020-05-21 …
1.已知a.b.c为实数,且a+b分之aXb=三分之一,b+c分之bXc=四分之一,a+c分之aX 2020-06-27 …