在梯形ABCD中，AD∥BC，又ADBC=12，点M在边AB，且使AMMB=23，点N在边CD上，使线段MN把梯形分成面积比为3：1的两部分，求CNND的值．

Question

在梯形ABCD中，AD∥BC，又(AD)/(BC)=(1)/(2)，点M在边AB，且使(AM)/(MB)=(2)/(3)，点N在边CD上，使线段MN把梯形分成面积比为3：1的两部分，求(CN)/(ND)的值．
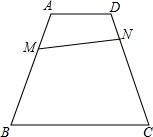在梯形ABCD中，AD∥BC，又(AD)/(BC)=(1)/(2)，点M在边AB，且使(AM)/(MB)=(2)/(3)，点N在边CD上，使线段MN把梯形分成面积比为3：1的两部分，求(CN)/(ND)的值．
(AD)/(BC)=(1)/(2)，点M在边AB，且使(AM)/(MB)=(2)/(3)，点N在边CD上，使线段MN把梯形分成面积比为3：1的两部分，求(CN)/(ND)的值．
(AD)/(BC)ADBCADADBCBC(1)/(2)，点M在边AB，且使(AM)/(MB)=(2)/(3)，点N在边CD上，使线段MN把梯形分成面积比为3：1的两部分，求(CN)/(ND)的值．
(1)/(2)121122(AM)/(MB)=(2)/(3)，点N在边CD上，使线段MN把梯形分成面积比为3：1的两部分，求(CN)/(ND)的值．
(AM)/(MB)AMMBAMAMMBMB(2)/(3)，点N在边CD上，使线段MN把梯形分成面积比为3：1的两部分，求(CN)/(ND)的值．
(2)/(3)232233(CN)/(ND)的值．
(CN)/(ND)CNNDCNCNNDND

Answer 1

如图，连结MC，MD，过M作梯形的高GH，分别交AD的延长线，BC于点G，H．

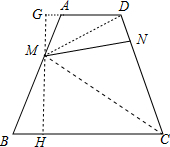
设AD=x，则BC=2x，设GH=5h，则MH=3h，MG=2h
∴S_梯形ABCD梯形ABCD=(1)/(2)（x+2x）×5h=7.5xh
S_△AMD=(1)/(2)AD×MG=(1)/(2)x•2h=xh，
S_△MBC=(1)/(2)BC×MH=(1)/(2)×2x•3h=3xh，
①当S_{四边形AMND}：S_{四边形BCNM}=1：3时，
∵S_△AMD：S_△MBC=xh：3xh=1：3，
∴S_△MDN：S_△MCN=1：3，
∵S_△MDN和S_△MCN高相等，
∴(DN)/(CN)=(1)/(3)，即(CN)/(ND)=3；
②当S_{四边形AMND}：S_{四边形BCNM}=3：1时，
∴S_{四边形AMND}=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (1)/(2)12111222（x+2x）×5h=7.5xh
S_△AMD△AMD=(1)/(2)AD×MG=(1)/(2)x•2h=xh，
S_△MBC=(1)/(2)BC×MH=(1)/(2)×2x•3h=3xh，
①当S_{四边形AMND}：S_{四边形BCNM}=1：3时，
∵S_△AMD：S_△MBC=xh：3xh=1：3，
∴S_△MDN：S_△MCN=1：3，
∵S_△MDN和S_△MCN高相等，
∴(DN)/(CN)=(1)/(3)，即(CN)/(ND)=3；
②当S_{四边形AMND}：S_{四边形BCNM}=3：1时，
∴S_{四边形AMND}=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (1)/(2)12111222AD×MG=(1)/(2)x•2h=xh，
S_△MBC=(1)/(2)BC×MH=(1)/(2)×2x•3h=3xh，
①当S_{四边形AMND}：S_{四边形BCNM}=1：3时，
∵S_△AMD：S_△MBC=xh：3xh=1：3，
∴S_△MDN：S_△MCN=1：3，
∵S_△MDN和S_△MCN高相等，
∴(DN)/(CN)=(1)/(3)，即(CN)/(ND)=3；
②当S_{四边形AMND}：S_{四边形BCNM}=3：1时，
∴S_{四边形AMND}=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (1)/(2)12111222x•2h=xh，
S_△MBC△MBC=(1)/(2)BC×MH=(1)/(2)×2x•3h=3xh，
①当S_{四边形AMND}：S_{四边形BCNM}=1：3时，
∵S_△AMD：S_△MBC=xh：3xh=1：3，
∴S_△MDN：S_△MCN=1：3，
∵S_△MDN和S_△MCN高相等，
∴(DN)/(CN)=(1)/(3)，即(CN)/(ND)=3；
②当S_{四边形AMND}：S_{四边形BCNM}=3：1时，
∴S_{四边形AMND}=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (1)/(2)12111222BC×MH=(1)/(2)×2x•3h=3xh，
①当S_{四边形AMND}：S_{四边形BCNM}=1：3时，
∵S_△AMD：S_△MBC=xh：3xh=1：3，
∴S_△MDN：S_△MCN=1：3，
∵S_△MDN和S_△MCN高相等，
∴(DN)/(CN)=(1)/(3)，即(CN)/(ND)=3；
②当S_{四边形AMND}：S_{四边形BCNM}=3：1时，
∴S_{四边形AMND}=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (1)/(2)12111222×2x•3h=3xh，
①当S_{四边形AMND}四边形AMND：S_{四边形BCNM}四边形BCNM=1：3时，
∵S_△AMD△AMD：S_△MBC△MBC=xh：3xh=1：3，
∴S_△MDN△MDN：S_△MCN△MCN=1：3，
∵S_△MDN△MDN和S_△MCN△MCN高相等，
∴(DN)/(CN)=(1)/(3)，即(CN)/(ND)=3；
②当S_{四边形AMND}：S_{四边形BCNM}=3：1时，
∴S_{四边形AMND}=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (DN)/(CN)DNCNDNDNDNCNCNCN=(1)/(3)，即(CN)/(ND)=3；
②当S_{四边形AMND}：S_{四边形BCNM}=3：1时，
∴S_{四边形AMND}=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (1)/(3)13111333，即(CN)/(ND)=3；
②当S_{四边形AMND}：S_{四边形BCNM}=3：1时，
∴S_{四边形AMND}=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (CN)/(ND)CNNDCNCNCNNDNDND=3；
②当S_{四边形AMND}四边形AMND：S_{四边形BCNM}四边形BCNM=3：1时，
∴S_{四边形AMND}四边形AMND=7.5xh×(3)/(4)=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (3)/(4)34333444=(45xh)/(8)，
S_{四边形BCNM}=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (45xh)/(8)45xh845xh45xh45xh888，
S_{四边形BCNM}四边形BCNM=7.5xh×(1)/(4)=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (1)/(4)14111444=(15xh)/(8)<S_△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (15xh)/(8)15xh815xh15xh15xh888△MBC△MBC，因此不合题意．
综上所述(CN)/(ND)=3． (CN)/(ND)CNNDCNCNCNNDNDND=3．