早教吧作业答案频道 -->数学-->
如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.(1)求证:AD2=BG•DH;(2)求证:CE=2DG;(3)求证:EF=2HG.
题目详情
如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.
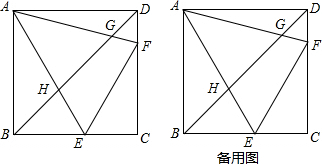
(1)求证:AD2=BG•DH;
(2)求证:CE=
DG;
(3)求证:EF=
HG.

(1)求证:AD2=BG•DH;
(2)求证:CE=
| 2 |
(3)求证:EF=
| 2 |
▼优质解答
答案和解析
证明:(1)∵四边形ABCD为正方形
∴∠ABD=∠ADB=45°,AB=AD,
∵∠EAF=45°
∴∠BAG=45°+∠BAH,∠AHD=45°+∠BAH,
∴∠BAG=∠AHD,
又∵∠ABD=∠ADB=45°,
∴△ABG∽△HDA,
∴
=
,
∴BG•DH=AB•AD=AD2;
(2)如图,连接AC,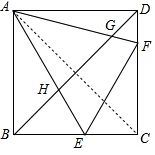
∵四边形ABCD是正方形
∴∠ACE=∠ADB=∠CAD=45°,
∴AC=
AD,
∵∠EAF=45°,
∴∠EAF=∠CAD,
∴∠EAF-∠CAF=∠CAD-∠CAF,
∴∠EAC=∠GAD,
∴△EAC∽△GAD,
∴
=
=
,
∴CE=
DG;
(3)由(2)得:△EAC∽△GAD,
∴
=
=
,
同理得:△AFC∽△AHB,
∴
=
=
,
∴
=
=
,
∴
=
,
∵∠GAH=∠EAF,
∴△GAH∽△EAF,
∴
=
,
∴EF=
GH.
∴∠ABD=∠ADB=45°,AB=AD,
∵∠EAF=45°
∴∠BAG=45°+∠BAH,∠AHD=45°+∠BAH,
∴∠BAG=∠AHD,
又∵∠ABD=∠ADB=45°,
∴△ABG∽△HDA,
∴
| AB |
| DH |
| BG |
| DA |
∴BG•DH=AB•AD=AD2;
(2)如图,连接AC,

∵四边形ABCD是正方形
∴∠ACE=∠ADB=∠CAD=45°,
∴AC=
| 2 |
∵∠EAF=45°,
∴∠EAF=∠CAD,
∴∠EAF-∠CAF=∠CAD-∠CAF,
∴∠EAC=∠GAD,
∴△EAC∽△GAD,
∴
| CE |
| DG |
| AC |
| AD |
| 2 |
∴CE=
| 2 |
(3)由(2)得:△EAC∽△GAD,
∴
| AE |
| AG |
| AC |
| AD |
| 2 |
同理得:△AFC∽△AHB,
∴
| AF |
| AH |
| AC |
| AB |
| 2 |
∴
| AE |
| AG |
| AF |
| AH |
| 2 |
∴
| AE |
| AG |
| AF |
| AH |
∵∠GAH=∠EAF,
∴△GAH∽△EAF,
∴
| EF |
| GH |
| 2 |
∴EF=
| 2 |
看了 如图,正方形ABCD,∠EA...的网友还看了以下:
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
limh→0(In(e+h)-1)/h因为是0/0型的,所以我用洛必达法则,求导后是不是(e+1) 2020-05-23 …
德布罗意波长公式求教注:v频率E=hνv=c/λ所以E=hc/λh/λ=E/cp=hν/cc=vλ 2020-06-22 …
如图,△ABC中,AD平分∠BAC,EF⊥AD交AB于点E,交AC于点F,交BC的延长线于点H.求 2020-06-27 …
f(x),g(x),h(x)在[a,b]上连续,(a,b)上可导,求证存在一个e属于(a,b)使得 2020-07-16 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.( 2020-07-19 …
各位帮我解一题九宫图用0到9的数字填进九宫图的A到IABCDEFGHI要求:A+B+C=D+E+F= 2020-11-02 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.(e 2020-11-19 …
A+B+C=84,D+E+F=111,H+I+J=138,A+D+H=124,B+E+I=148,C 2020-12-14 …
求物理大神!公式推导的问题(E=mc^2)E=mc^2……①E=hν………②然后得到h/mc=λ但是 2021-01-07 …