早教吧作业答案频道 -->数学-->
己知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG(1)求证:∠AFD+∠CBG=180°;(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB
题目详情
己知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:∠AFD+∠CBG=180°;
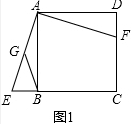
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
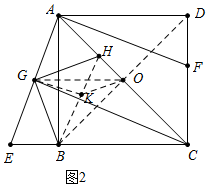
(3)如图3,连接HF,若CH=3AH,AD=2
,求线段HF的长.
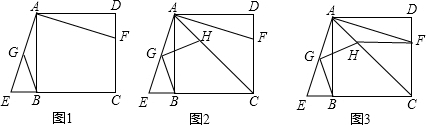
(1)求证:∠AFD+∠CBG=180°;
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2
| 10 |

▼优质解答
答案和解析
(1)证明:如图1中,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠AEF=90°,
∴∠EAB=∠DAF,
∵∠ABE=∠ADF=90°,
∴△ABE≌△ADF,
∴∠AFD=∠E,
∵AG=GE,
∴GB=GE=GA,
∴∠E=∠GBE=∠AFD,
∵∠GBE+∠GBC=180°,
∴∠AFD+∠GBC=180°.
(2)证明:如图2中,连接BD交AC于O,连接OG、BH、取BH的中点K,连接GK、OK.
∵∠BGH=∠BOH=90°,BK=KH,
∴GK=KH=OK=KB,
∴O、H、G、B四点共圆,
∵AG=GE,AO=OC.
∴OG∥CE,
∴∠GOB=∠OBC=45°,
∴∠GOH=∠GBH=45°,∵∠BGH=90°,
∴∠GBH=∠GHB=45°,
∴GH=GB.
(3) 如图3中,如图3中,设OG交AB于T,GH交AB于P.,作HM⊥DF于M.
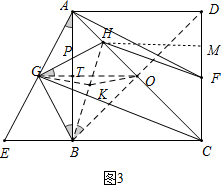
∵OG∥EC,
AB⊥CE,
∴OG⊥AB,
易证∠EAB=∠GBP=∠PGT=∠HBO,
∴tan∠EAB=tan∠HBO=
,
∵CH=3AH,OA=OC=OB,
∴tan∠EAB=tan∠HBO=
=
,
∵AB=AD=2
,
∴BE=DF=
,
在Rt△HMF中,易证FM=
,HM=
,
∴HF=
=5.

∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠AEF=90°,
∴∠EAB=∠DAF,
∵∠ABE=∠ADF=90°,
∴△ABE≌△ADF,
∴∠AFD=∠E,
∵AG=GE,
∴GB=GE=GA,
∴∠E=∠GBE=∠AFD,
∵∠GBE+∠GBC=180°,
∴∠AFD+∠GBC=180°.
(2)证明:如图2中,连接BD交AC于O,连接OG、BH、取BH的中点K,连接GK、OK.

∵∠BGH=∠BOH=90°,BK=KH,
∴GK=KH=OK=KB,
∴O、H、G、B四点共圆,
∵AG=GE,AO=OC.
∴OG∥CE,
∴∠GOB=∠OBC=45°,
∴∠GOH=∠GBH=45°,∵∠BGH=90°,
∴∠GBH=∠GHB=45°,
∴GH=GB.
(3) 如图3中,如图3中,设OG交AB于T,GH交AB于P.,作HM⊥DF于M.

∵OG∥EC,
AB⊥CE,
∴OG⊥AB,
易证∠EAB=∠GBP=∠PGT=∠HBO,
∴tan∠EAB=tan∠HBO=
| HO |
| OB |
∵CH=3AH,OA=OC=OB,
∴tan∠EAB=tan∠HBO=
| HO |
| OB |
| 1 |
| 2 |
∵AB=AD=2
| 10 |
∴BE=DF=
| 10 |
在Rt△HMF中,易证FM=
| ||
| 2 |
| 3 |
| 2 |
| 10 |
∴HF=
| HM2+FM2 |
看了 己知:如图1.正方形ABCD...的网友还看了以下:
求合适的成语,形容一个人的行为.A,B,C三个人,A和C是仇人,但是B和A与C关系都特别好,A,C 2020-05-15 …
己知多项式x²+ax²+bx+c能被x²+3x-4整除 ①求4a+c的值 ②求2a-2b-c的值 2020-05-16 …
求证:直角三角形两直角边之和小于小斜边与斜边上的高的和算了,我让自己回答吧!设三边为a,b,c,c 2020-05-23 …
在△ABC中,角A,B,C所对的边分别是a,b,c.己知(b-2a)cosC+ccosB=0.(1 2020-07-08 …
(1)A,B,C大于0求A/B+3C+B/8C+4A+9C/3A+2B的最小值(2)A,B,C,D 2020-07-09 …
己知:如图,在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC.(1)若∠B=50°,∠C 2020-07-16 …
在△ABC中,角A,B,C所对的边分别是a,b,c.己知csinA=acosC.(I)求C;(II 2020-07-20 …
对待自身的优缺点,我们应有的态度是()A.只看到自己的优点,不承认自己的缺点B.夸大自己的优点,缩 2020-07-26 …
能够正确的认识和评价自己,是一个人心理成熟的标志之一.正确评价自己的关键是()A.扬长避短,更多的看 2020-12-10 …
“在谋求自己发展的同时,也要帮助别人发展。”这句话是在解释[]A.己所欲,施于人B.己所不欲,勿施 2021-01-12 …