早教吧作业答案频道 -->数学-->
已知点A、B分别在x轴,y轴上,OA=OB,点C为AB的中点,AB=122(1)如图1,求点C的坐标;(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;(3)在条件(2)中,若点E的坐标为(
题目详情
已知点A、B分别在x轴,y轴上,OA=OB,点C为AB的中点,AB=12
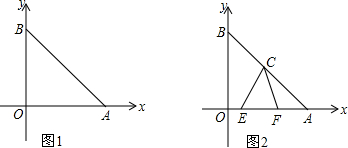
(1)如图1,求点C的坐标;
(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;
(3)在条件(2)中,若点E的坐标为(3,0),求CF的长.
| 2 |
(1)如图1,求点C的坐标;
(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;
(3)在条件(2)中,若点E的坐标为(3,0),求CF的长.

▼优质解答
答案和解析
(1)连接OC,作CM⊥OA于点M,如图1所示.
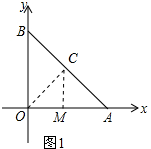
∵OA=OB,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴OA=OB=12.
∵点C为线段AB的中点,
∴OC⊥AB,
∴△OCA为等腰直角三角形,
又∵CM⊥OA,
∴CM=OM=MA=
OA=6.
故点C的坐标为(6,6).
(2)证明:连接OC,在OB上截取OM=AF,连接CM、ME,如图2所示.
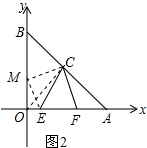
∵△AOB、△OCA、△OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC.
在△ACF和△OCM中,
,
∴△ACF≌△OCM(SAS),
∴CM=CF,∠OCM=∠ACF.
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF.
在△ECF和△ECM中,
,
∴△ECF≌△ECM(SAS),
∴ME=EF.
在Rt△MOE中,∠MOE=90°,
∴EF2=ME2=OE2+OM2=OE2+AF2.
(3)过点C作CN⊥OA于点N,如图3所示.
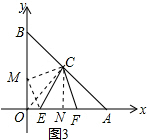
设AF=x=OM,则EF=OA-OE-AF=12-3-x=9-x=EM,
由(2)可得:(9-x)2=32+x2,
解得:x=4,
∴OF=OA-AF=12-4=8.
∵△OCA为等腰直角三角形,
∴CN=ON=
OA=6,NF=OF-ON=8-6=2.
在Rt△CNF中,∠CNF=90°,CN=6,NF=2,
∴CF=
=2
.

∵OA=OB,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴OA=OB=12.
∵点C为线段AB的中点,
∴OC⊥AB,
∴△OCA为等腰直角三角形,
又∵CM⊥OA,
∴CM=OM=MA=
| 1 |
| 2 |
故点C的坐标为(6,6).
(2)证明:连接OC,在OB上截取OM=AF,连接CM、ME,如图2所示.

∵△AOB、△OCA、△OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC.
在△ACF和△OCM中,
|
∴△ACF≌△OCM(SAS),
∴CM=CF,∠OCM=∠ACF.
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF.
在△ECF和△ECM中,
|
∴△ECF≌△ECM(SAS),
∴ME=EF.
在Rt△MOE中,∠MOE=90°,
∴EF2=ME2=OE2+OM2=OE2+AF2.
(3)过点C作CN⊥OA于点N,如图3所示.

设AF=x=OM,则EF=OA-OE-AF=12-3-x=9-x=EM,
由(2)可得:(9-x)2=32+x2,
解得:x=4,
∴OF=OA-AF=12-4=8.
∵△OCA为等腰直角三角形,
∴CN=ON=
| 1 |
| 2 |
在Rt△CNF中,∠CNF=90°,CN=6,NF=2,
∴CF=
| CN2+NF2 |
| 10 |
看了 已知点A、B分别在x轴,y轴...的网友还看了以下:
圆锥曲线的已知椭圆C:x^2/2+y^2=1的右焦点为F,右准线为l,点A属于l,线段AF交C于点 2020-04-08 …
坐标系中,已知点A(-2,0),B(0,4),C(0,3),过点C交x轴于点D,使得以D,O,C为 2020-06-03 …
已知:a=-1,b=1,c=5.a,b,c所对应的点分别A,B,C.为点P为易动点,其对应的数为x 2020-06-12 …
在平面直角坐标系中,已知点A(-2,0),B(2,0),若在坐标轴上存在点C,使得AC+BC=m, 2020-07-30 …
同时掷两颗骰子,X,Y分别表示第一、二两颗骰子出现的点数,设事件A表示:“两颗骰子出现点数之和为奇数 2020-11-18 …
同时掷两颗骰子,x,y分别表示第一,二两颗骰子出现的点数,设事件A表示“两颗骰子出现点数之和为奇数” 2020-11-18 …
同时掷两颗骰子,x,y分别表示第一,二两颗骰子出现的点数,设事件A表示“两颗骰子出现点数之和为奇数” 2020-11-18 …
已知O、A、B、C为同一直线上的四点,求O与A的距离.已知O、A、B、C为同一直线上的四点,AB间的 2020-12-09 …
在平面直角坐标系中,已知点A(-2,0),B(2,0),若在坐标轴上存在点C,使得AC+BC=m,则 2021-01-12 …
在平面直角坐标系中,已知点A(-2,0),B(2,0),若在坐标轴上存在点C,使得AC+BC=m,则 2021-01-12 …